基于matlab的密度散点图绘制

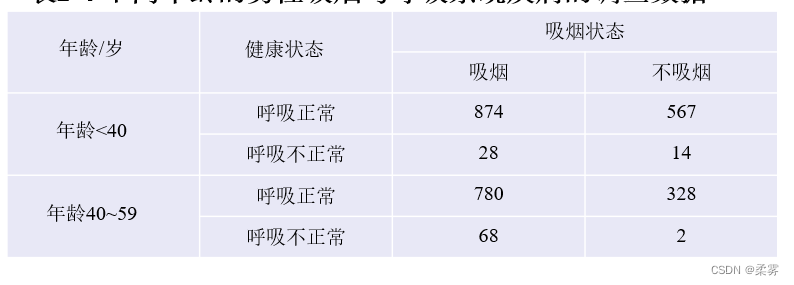
本文介绍: 基于matlab的密度散点图绘制

1. 什么是密度散点图？

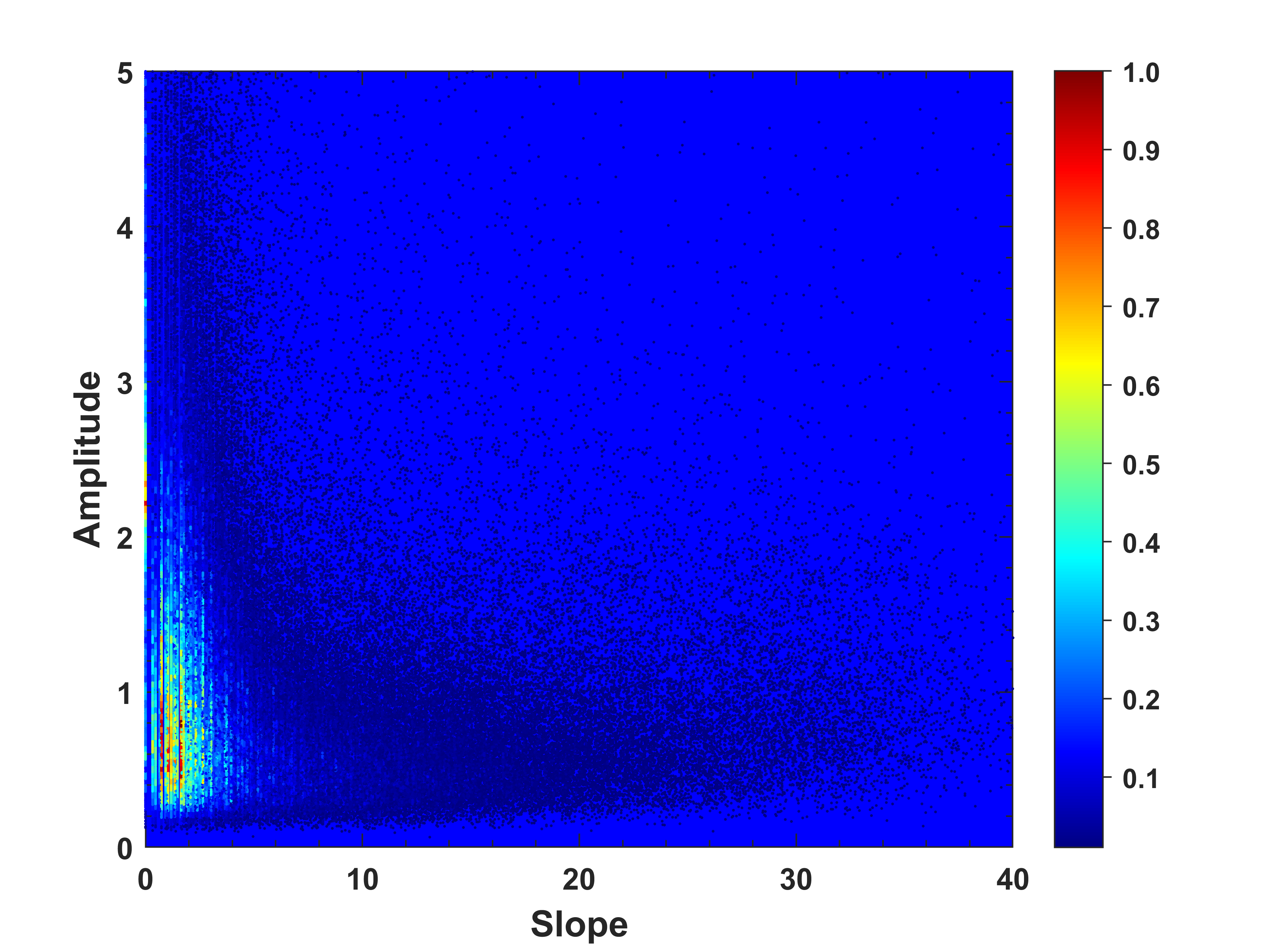
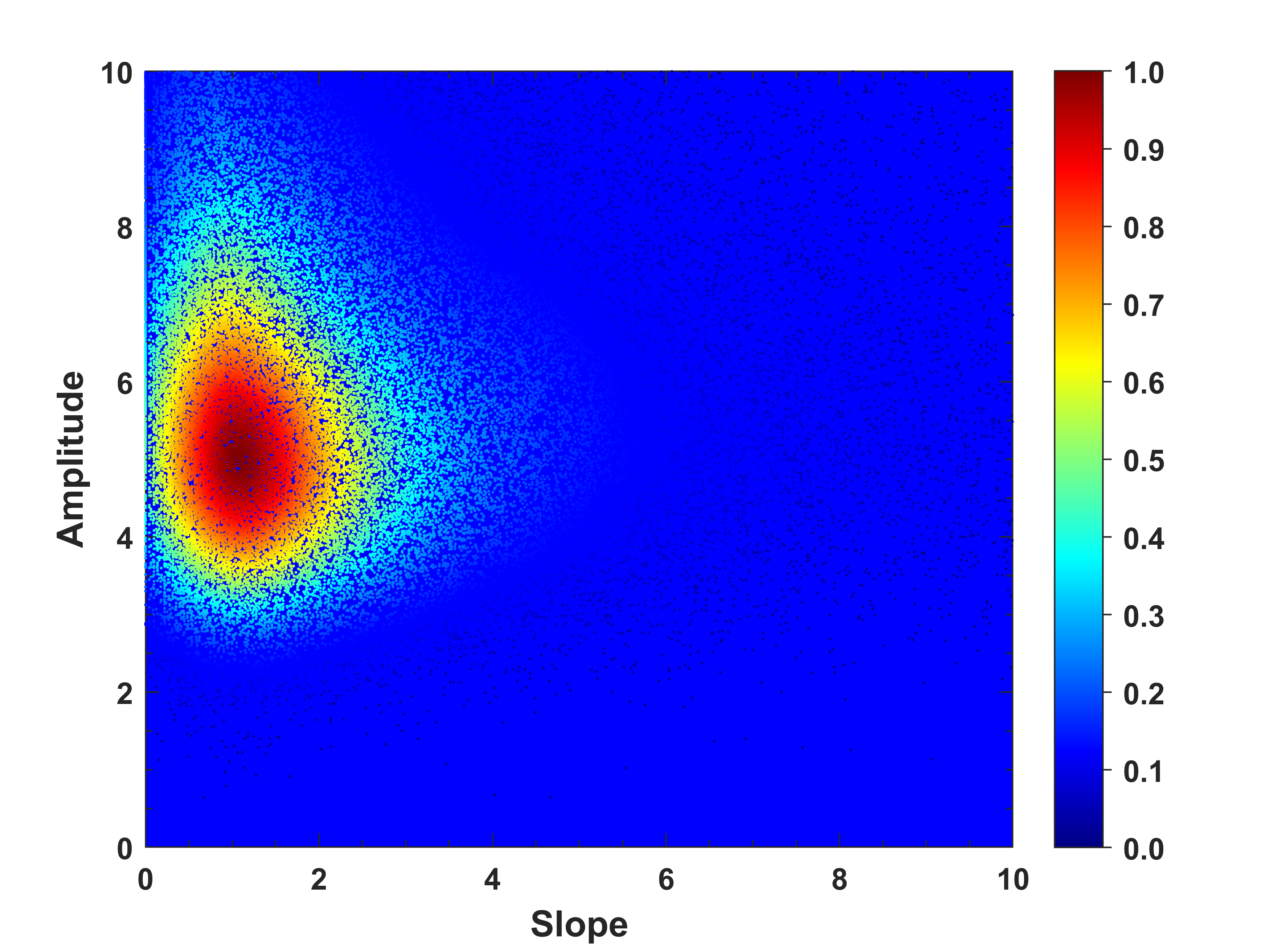
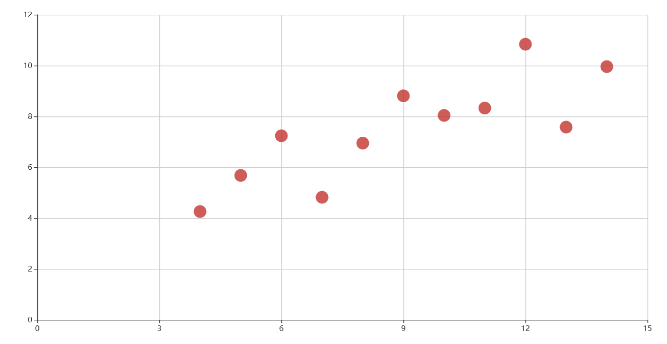
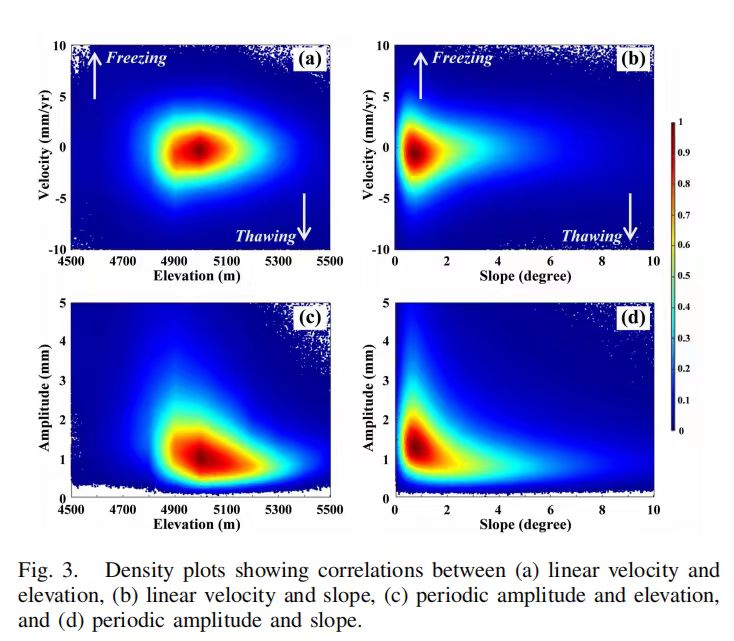
密度散点图就是在普通散点图的基础上，基于样本点一定范围的样本数计算该样本点的密度，以不同的颜色来显示样本点密度的大小，这样能够直观的显示出数据的空间聚集情况，如下图分别是二维和三维密度散点图

8425425e7e3938936bf724a74fc0402

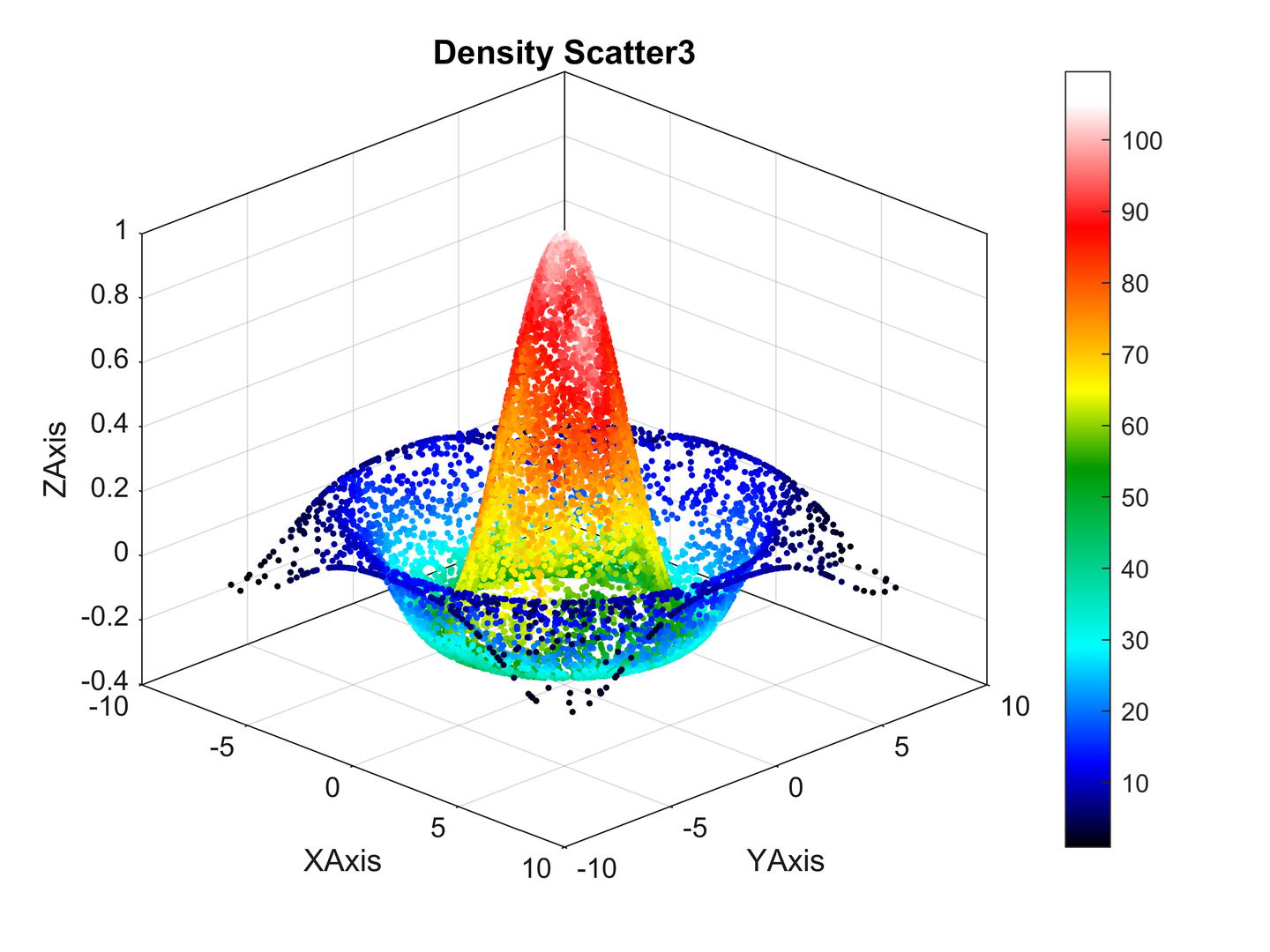
Matlab进阶绘图第25期—三维密度散点图

2. 密度散点图绘制思路

2.1 网格划分

以二维散点图为例，将坐标轴范围划分为一系列大小相同的格网，统计每一个格网内部的样本点数除以格网面积，将所得结果作为该格网内样本点的密度，根据实际需要决定是否需要将密度进行归一化处理，这种方法计算量小，效率高，但效果相对较差

2.2 空间搜索

以二维散点图为例，对某一样本点搜索给定半径范围内的样本数，样本数除以搜索圆的面积作为样本点的密度，同样根据实际使用需要决定是否需要将密度进行归一化处理，这种方法计算量大，效率较低，但效果更好

3. matlab绘制密度散点图

基于网格划分的密度计算函数

function density = density_Grid(data,nd)
% 功能：利用格网划分提取离散点密度特征
% 输入：data   - 原始数据
% 输入：nd - 划分格网数
% 输出：density - 样本密度向量 
M = size(data,1);
N = size(data,2);
data_max = max(data);
data_min = min(data);
data_interval = (data_max - data_min)/nd;
if N == 2
    data_freq = zeros(nd,nd);
    data_index = zeros(M,N);
    for i = 1:M
        x = data(i,1);
        y = data(i,2);
        c = min(floor((x - data_min(1))/data_interval(1))+1,nd);
        r = min(floor((data_max(2)-y)/data_interval(2))+1,nd);
        data_freq(r,c) = data_freq(r,c)+1;
        data_index(i,:) = [r,c]; 
    end
else
    data_freq = zeros(nd,nd,nd);
    for i = 1:M
        x = data(i,1);
        y = data(i,2);
        z = data(i,3);
        c = min(floor((x - data_min(1))/data_interval(1))+1,nd);
        r = min(floor((data_max(2)-y)/data_interval(2))+1,nd);
        v = min(floor((z - data_min(3))/data_interval(3))+1,nd);
        data_freq(r,c,v) = data_freq(r,c,v)+1;
        data_index(i,:) = [r,c,v];
    end
end
s = 1;
for i = 1:N
    s = s * data_interval(i);
end
data_freq = data_freq./s;
density = zeros(M,1);
if N==2
    for i = 1:M
        r = data_index(i,1);
        c = data_index(i,2);
        density(i,1) = data_freq(r,c);
    end
else
    for i = 1:M
        r = data_index(i,1);
        c = data_index(i,2);
        v = data_index(i,3);
        density(i,1) = data_freq(r,c,v);
    end
end
% 密度归一化
max_density = max(density);
density = density./max_density;
end

基于空间搜索的密度计算函数

function density = density_KD(data,radius)
% 功能：利用KD树提取离散点密度特征
% 输入：data   - 原始数据
% 输入：radius - 搜索半径
% 输出：density - 样本密度向量 
M = size(data,1);
N = size(data,2);
density = zeros(M,1);
idx = rangesearch(data(:,1:N),data(:,1:N),radius,'Distance','euclidean','NSMethod','kdtree');
if N=2
	s = pi*radius^2
else
	s = 3/4*pi*radius^3
end
for i = 1:M
    density(i,1) = length(idx{i})/s;
end
% 密度归一化
max_density = max(density);
density = density./max_density;
end

绘图函数

% 数据读取
% xbly_data = readtable("xiboliya.xlsx");
% xbly_data = table2array(xbly_data)
% xbly_a = xbly_data(:,2);
% xbly_dem = xbly_data(:,3);
% xbly_slope = xbly_data(:,4);
% xbly_ndvi = xbly_data(:,5);
% scatterDensity(xbly_slope(1:10:528523),xbly_a(1:10:528523),"slope","a")
function scatterDensity(x,y,xtitle,ytitle)
data=[x,y];
density_2D = density_KD(data(:,1:2),1);%将density2D_KD放在该代码同一路径下
% density_2D = density_Grid(data(:,1:2),40000);
scatter(x,y,10, density_2D, '.');
%设置色带
colormap('jet');
hXLabel = xlabel(xtitle);
hYLabel = ylabel(ytitle);
% 坐标轴美化
set(gca, 'Box', 'on', ...                                        % 边框
        'XGrid', 'off', 'YGrid', 'off', ...                      % 网格
        'TickDir', 'in', 'TickLength', [.015 .015], ...          % 刻度
        'XMinorTick', 'on', 'YMinorTick', 'on', 'YTick', 0:2:10,'YLim', [0,10]);            % 小刻度
% 字体和字号
set(gca, 'FontName', 'TimesNewRoma')
set([hXLabel, hYLabel],'FontName', 'TimesNewRoma')
set(gca, 'FontSize', 10)
set(gca, 'FontName', 'TimesNewRoma')
set([hXLabel, hYLabel],'FontSize', 11)
% 背景颜色
set(gca,'Color',[0 0 1]);
%设置色带显示
c = colorbar;
set(c,'tickdir','out');
%色带坐标范围及显示间隔
set(c,'YTick',0:0.2:1.0); 
% 保存结果
% saveas(gcf,strcat(xtitle,"_",ytitle,".fig"));
end