本文介绍: 这个解法实际上就是改造一下非递归后序遍历的代码,因为每次遍历都会将节点入栈,我们只需要在弹栈之前,记录一下栈的大小,取最大值就好。最大深度也可以用层序遍历来写,因为层序遍历就是遍历每一层嘛,最大深度就遍历到最后一层,最小深度就遍历到第一个叶子节点就好了。如果两个值相等,不代表一定对称,还需要继续检查左节点的左节点和右节点的右节点、左节点的右节点和右节点的左节点是否相等。要求这棵树的最大深度,我们只需要求左子树和右子树的深度,然后取最大值加一就好,同样地对每个节点都如此,于是就可以用递归来解。
1、101. 对称二叉树
检查是否对称,其实就是检查左节点等不等于右节点,我们可以用递归来做。
如果左右节点都为null,说明肯定对称呀,返回true。
如果一个为null一个不为null,或者左右的值不相等,则为false。(这里简化一下,比如
left==null&&right!=null可以只写left==null,因为如果都为null,会进入第一个if)。
如果两个值相等,不代表一定对称,还需要继续检查左节点的左节点和右节点的右节点、左节点的右节点和右节点的左节点是否相等。
2、104. 二叉树的最大深度
递归解法
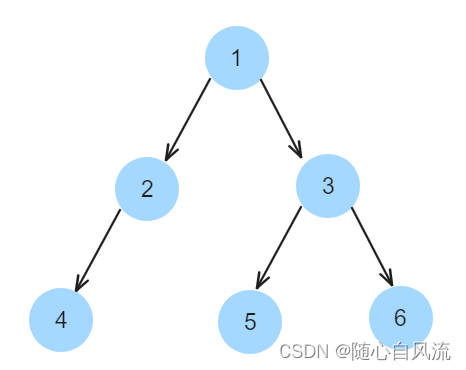
迭代解法
3、111. 二叉树的最小深度
递归解法
层序遍历
4、 226. 翻转二叉树
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。