Improve NN
文章目录
train/dev/test set
0.7/0/0.3 0.6.0.2.0.2 -> 100-10000
0.98/0.01/0.01 … -> big data
Bias/Variance
偏差度量的是单个模型的学习能力,而方差度量的是同一个模型在不同数据集上的稳定性。
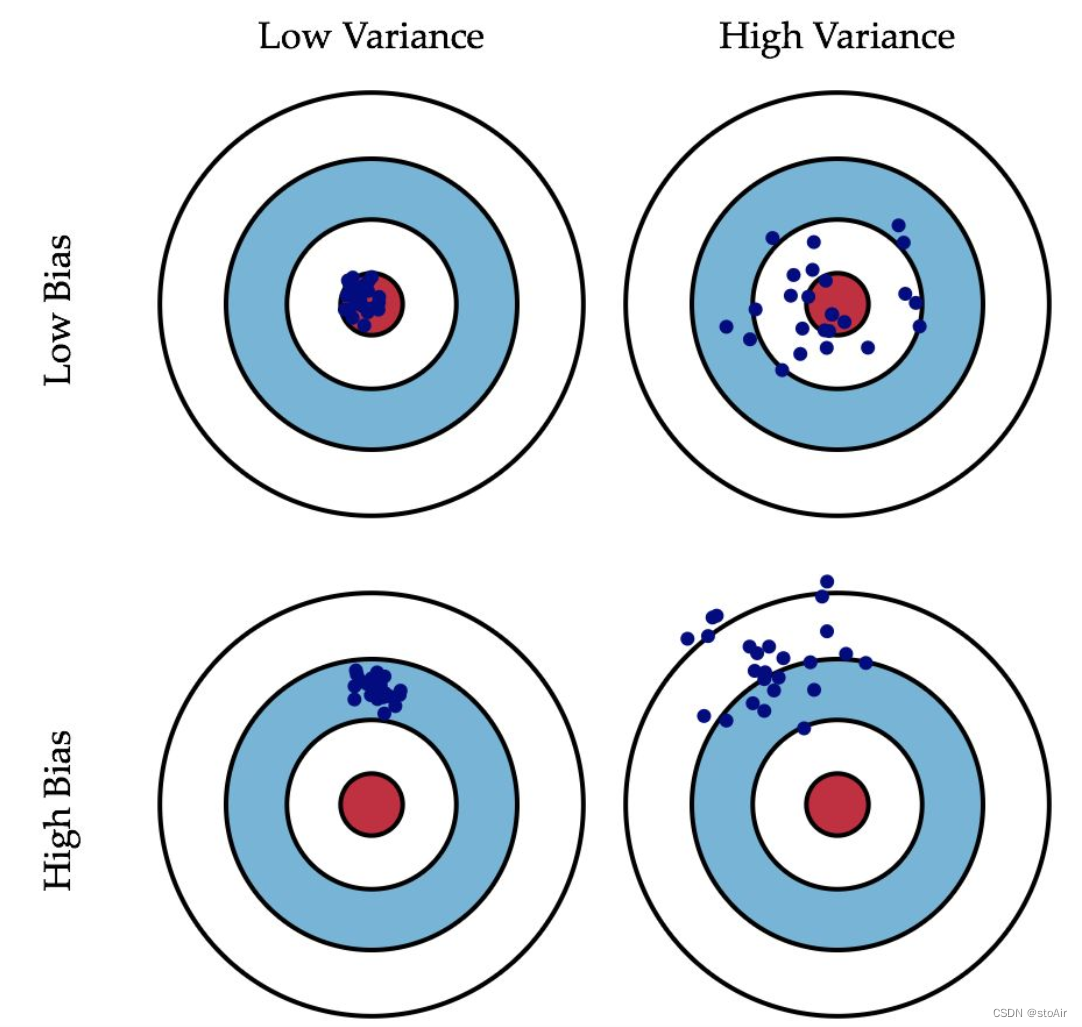
high variance ->high dev set error
high bias ->high train set error
basic recipe
high bias -> bigger network / train longer / more advanced optimization algorithms / NN architectures
high variance -> more data / regularization / NN architecture
Regularization
Logistic Regression
L
2
r
e
g
u
l
a
r
i
z
a
t
i
o
n
:
m
i
n
J
(
w
,
b
)
→
J
(
w
,
b
)
=
1
m
∑
i
=
1
m
L
(
y
^
(
i
)
,
y
(
i
)
)
+
λ
2
m
∥
w
∥
2
2
L2;; regularization:\minmathcal{J}(w,b)rightarrow J(w,b)=frac{1}{m}sum_{i=1}^mmathcal{L}(hat y^{(i)},y^{(i)})+frac{lambda}{2m}Vert wVert_2^2
L2regularization:minJ(w,b)→J(w,b)=m1i=1∑mL(y^(i),y(i))+2mλ∥w∥22
Neural network
F
r
o
b
e
n
i
u
s
n
o
r
m
∥
w
[
l
]
∥
F
2
=
∑
i
=
1
n
[
l
]
∑
j
=
1
n
[
l
−
1
]
(
w
i
,
j
[
l
]
)
2
D
r
o
p
o
u
t
r
e
g
u
l
a
r
i
z
a
t
i
o
n
:
d
3
=
n
p
.
r
a
n
d
m
.
r
a
n
d
(
a
3.
s
h
a
p
e
.
s
h
a
p
e
[
0
]
,
a
3.
s
h
a
p
e
[
1
]
<
k
e
e
p
.
p
r
o
b
)
a
3
=
n
p
.
m
u
l
t
i
p
l
y
(
a
3
,
d
3
)
a
3
/
=
k
e
e
p
.
p
r
o
b
Frobenius;; norm\ Vert w^{[l]}Vert^2_F=sum_{i=1}^{n^{[l]}}sum_{j=1}^{n^{[l-1]}}(w_{i,j}^{[l]})^2\\ Dropout;; regularization:\ d3=np.randm.rand(a3.shape.shape[0],a3.shape[1]<keep.prob)\ a3=np.multiply(a3,d3)\ a3/=keep.prob
Frobeniusnorm∥w[l]∥F2=i=1∑n[l]j=1∑n[l−1](wi,j[l])2Dropoutregularization:d3=np.randm.rand(a3.shape.shape[0],a3.shape[1]<keep.prob)a3=np.multiply(a3,d3)a3/=keep.prob
other ways
- early stopping
- data augmentation
optimization problem
speed up the training of your neural network
Normalizing inputs
- subtract mean
μ
=
1
m
∑
i
=
1
m
x
(
i
)
x
:
=
x
−
μ
mu =frac{1}{m}sum _{i=1}^{m}x^{(i)}\ x:=x-mu
μ=m1i=1∑mx(i)x:=x−μ
- normalize variance
σ
2
=
1
m
∑
i
=
1
m
(
x
(
i
)
)
2
x
/
=
σ
sigma ^2=frac{1}{m}sum_{i=1}^m(x^{(i)})^2\ x/=sigma
σ2=m1i=1∑m(x(i))2x/=σ
vanishing/exploding gradients
y
=
w
[
l
]
w
[
l
−
1
]
.
.
.
w
[
2
]
w
[
1
]
x
w
[
l
]
>
I
→
(
w
[
l
]
)
L
→
∞
w
[
l
]
<
I
→
(
w
[
l
]
)
L
→
0
y=w^{[l]}w^{[l-1]}…w^{[2]}w^{[1]}x\ w^{[l]}>Irightarrow (w^{[l]})^Lrightarrowinfty \w^{[l]}<Irightarrow (w^{[l]})^Lrightarrow0
y=w[l]w[l−1]…w[2]w[1]xw[l]>I→(w[l])L→∞w[l]<I→(w[l])L→0
weight initialize
v
a
r
(
w
)
=
1
n
(
l
−
1
)
w
[
l
]
=
n
p
.
r
a
n
d
o
m
.
r
a
n
d
n
(
s
h
a
p
e
)
∗
n
p
.
s
q
r
t
(
1
n
(
l
−
1
)
)
var(w)=frac{1}{n^{(l-1)}}\ w^{[l]}=np.random.randn(shape)*np.sqrt(frac{1}{n^{(l-1)}})
var(w)=n(l−1)1w[l]=np.random.randn(shape)∗np.sqrt(n(l−1)1)
gradient check
Numerical approximation
f
(
θ
)
=
θ
3
f
′
(
θ
)
=
f
(
θ
+
ε
)
−
f
(
θ
−
ε
)
2
ε
f(theta)=theta^3\ f'(theta)=frac{f(theta+varepsilon)-f(theta-varepsilon)}{2varepsilon}
f(θ)=θ3f′(θ)=2εf(θ+ε)−f(θ−ε)
grad check
d
θ
a
p
p
r
o
x
[
i
]
=
J
(
θ
1
,
.
.
.
θ
i
+
ε
.
.
.
)
−
J
(
θ
1
,
.
.
.
θ
i
−
ε
.
.
.
)
2
ε
=
d
θ
[
i
]
c
h
e
c
k
:
∥
d
θ
a
p
p
r
o
x
−
d
θ
∥
2
∥
d
θ
a
p
p
r
o
x
∥
2
+
∥
d
θ
∥
2
<
1
0
−
7
dtheta_{approx}[i]=frac{J(theta_1,…theta_i+varepsilon…)-J(theta_1,…theta_i-varepsilon…)}{2varepsilon}=dtheta[i]\ check:frac{Vert dtheta_{approx}-dthetaVert_2}{Vert dtheta_{approx}Vert_2+Vert dthetaVert_2}<10^{-7}
dθapprox[i]=2εJ(θ1,…θi+ε…)−J(θ1,…θi−ε…)=dθ[i]check:∥dθapprox∥2+∥dθ∥2∥dθapprox−dθ∥2<10−7
原文地址:https://blog.csdn.net/Star__01/article/details/136063994
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_67649.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!