梅氏定理和塞瓦定理
一、说明
在射影几何中,梅涅劳斯(Menelaus)定理和塞瓦定理是非常重要的基本定理。通过这两个定理,可以导出多项结论,如:极点-极线性质、德萨格定理、pascal定理等;本篇专门叙述这两个定理证明。及相关启发。
二、梅涅劳斯(Menelaus)定理
梅涅劳斯(Menelaus)定理(简称梅氏定理)最早出现在由古希腊数学家梅涅劳斯的著作《球面学》(Sphaerica)中。
定理定义
当一条直线交
Δ
A
B
C
Delta ABC
ΔABC三边所在的直线
B
C
,
A
C
,
A
B
BC,AC,AB
BC,AC,AB分别于点
D
,
E
,
F
D,E,F
D,E,F时,则有
A
F
F
B
B
D
D
C
C
E
E
A
=
1
frac{AF}{FB} frac{BD}{DC}frac{CE}{EA}=1
FBAFDCBDEACE=1
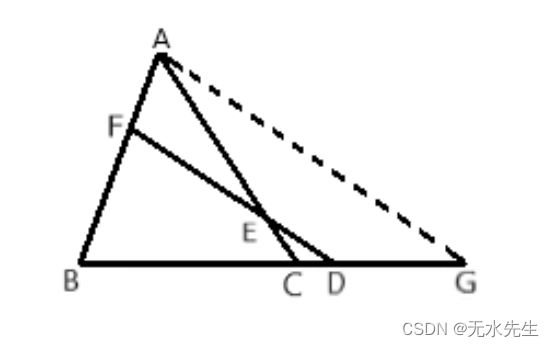
分析:显然,
D
,
E
,
F
D,E,F
D,E,F分别为线段
B
C
,
A
C
,
A
B
BC,AC,AB
BC,AC,AB的定比分点。因此:
A
F
F
B
=
λ
1
;
B
D
D
C
=
λ
2
;
C
E
E
A
=
λ
3
frac{AF}{FB}=lambda_1 ; ; frac{BD}{DC} =lambda_2;frac{CE}{EA}=lambda_3
FBAF=λ1;DCBD=λ2;EACE=λ3
因此,等价说法是:
λ
1
λ
2
λ
3
=
1
lambda_1 lambda_2lambda_3=1
A
G
∥
D
B
AGparallel DB
AG∥DB交
B
C
BC
BC的延长线于G点, 则:
A
F
F
B
=
λ
1
=
D
G
B
D
frac{AF}{FB}=lambda_1=frac{DG}{BD}
FBAF=λ1=BDDG
C
E
E
A
=
λ
3
=
C
D
D
G
frac{CE}{EA}=lambda_3=frac{CD}{DG}
EACE=λ3=DGCD
∴
A
F
F
B
B
D
D
C
C
E
E
A
=
λ
1
λ
2
λ
3
=
D
G
B
D
B
D
D
C
C
D
D
G
=
1
therefore frac{AF}{FB} frac{BD}{DC}frac{CE}{EA}= lambda_1 lambda_2lambda_3=frac{DG}{BD} frac{BD}{DC}frac{CD}{DG}=1
三、塞瓦(Giovanni Ceva)定理
四、塞瓦点的推广
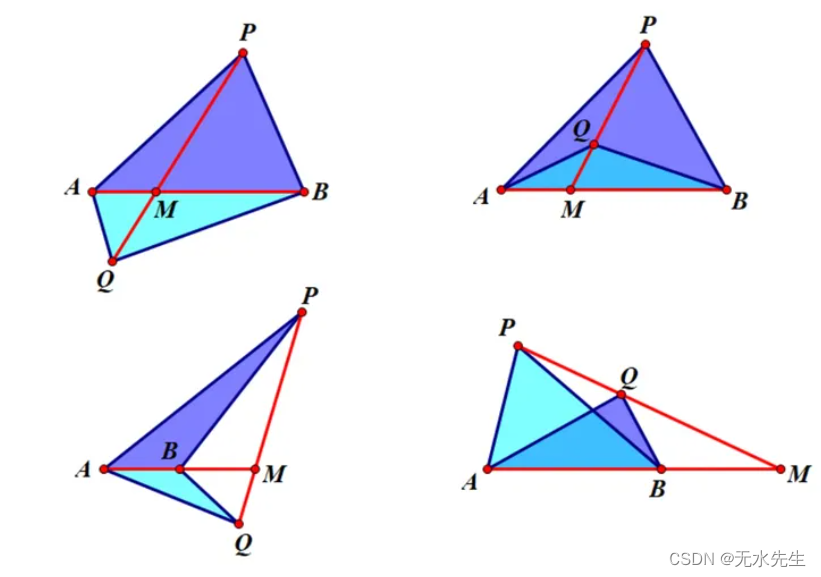
4.1 共线定理
P
M
Q
M
=
S
Δ
P
A
B
S
Δ
Q
A
B
frac{PM}{QM} = frac{S_{Delta PAB}}{S_{Delta QAB}}
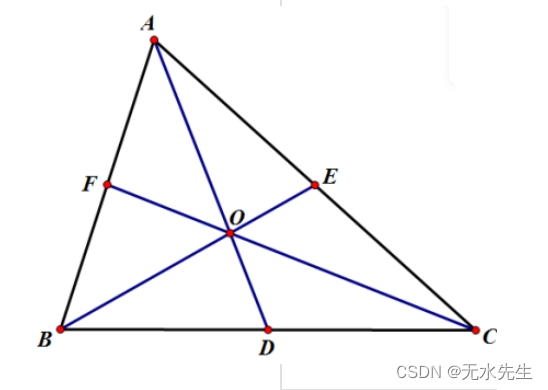
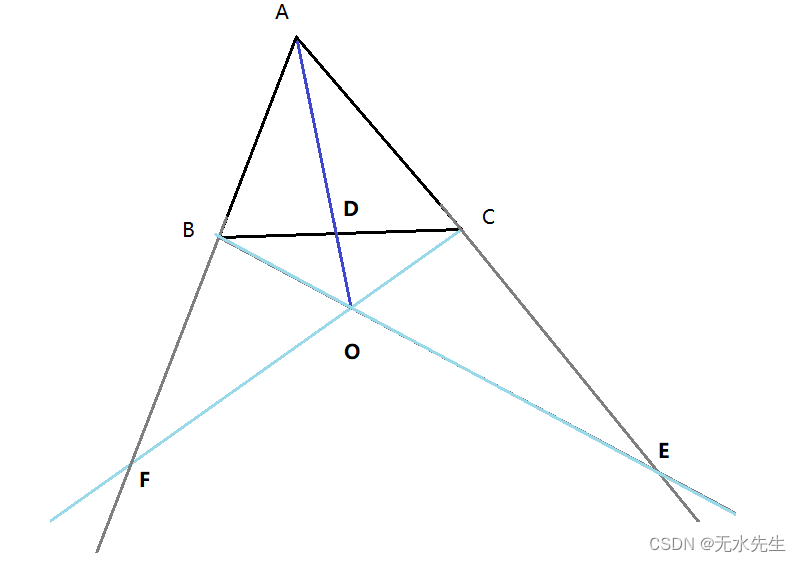
4.2 三角形外的塞瓦点
A
F
F
B
B
D
D
C
C
E
E
A
=
1
frac{AF}{FB} frac{BD}{DC}frac{CE}{EA}=1
B
D
D
C
=
S
Δ
A
B
D
−
S
Δ
O
B
D
S
Δ
A
D
C
−
S
Δ
O
B
D
=
S
Δ
O
B
A
S
Δ
C
A
O
frac{BD}{DC} = frac{S_{Delta ABD}-S_{Delta OBD}}{S_{Delta ADC}-S_{Delta OBD}} =frac{S_{Delta OBA}}{S_{Delta CAO}}
DCBD=SΔADC−SΔOBDSΔABD−SΔOBD=SΔCAOSΔOBA
C
E
E
A
=
S
Δ
B
C
O
S
Δ
A
B
O
frac{CE}{EA} = frac{S_{Delta BCO}}{S_{Delta ABO}}
EACE=SΔABOSΔBCO
A
F
F
B
=
S
Δ
C
A
O
S
Δ
B
C
O
frac{AF}{FB} = frac{S_{Delta CAO}}{S_{Delta BCO}}






![[软件工具]文档页数统计工具软件pdf统计页数word统计页数ppt统计页数图文打印店快速报价工具](https://img-blog.csdnimg.cn/direct/09dfbaff3e9a47a9a551dd65fef5d482.jpeg)