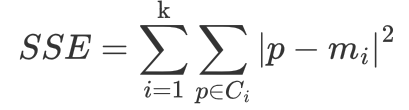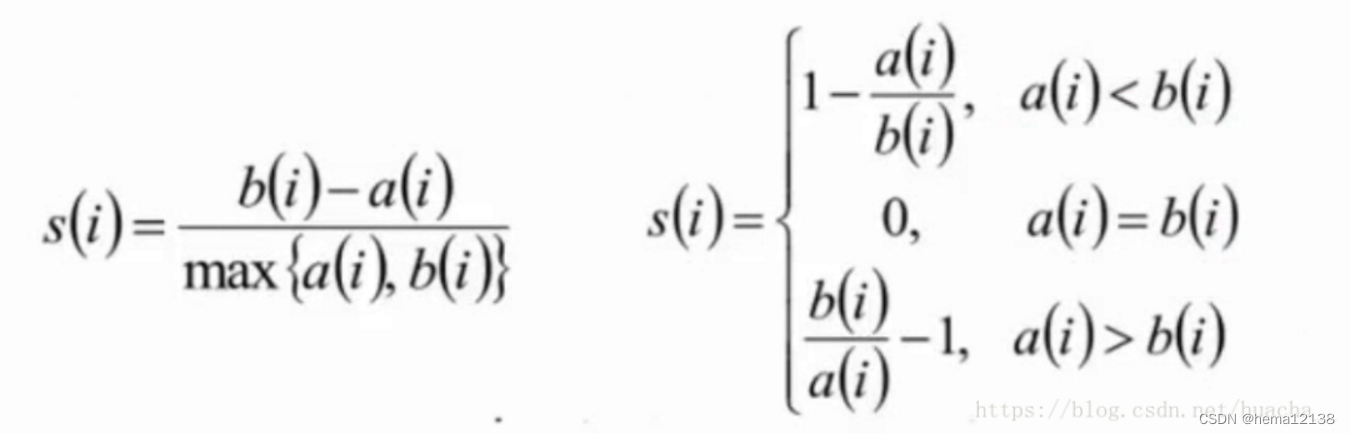机器学习本科课程实验6 聚类实验

本文介绍: # 第一题：使用sklearn的DBSCAN和AgglomerativeClustering完成聚类实验内容：1. 使用sklearn的DBSCAN和AgglomerativeClustering在两个数据集上完成聚类任务2. 对聚类结果可视化3. 对比外部指标FMI和NMI

其中,

$i$ 表示向量的第

$i$ 个分量。

我们要实现一个可以计算多个样本组成的矩阵

$X$ ，与某一个类中心

$y$ 之间欧氏距离的函数。

给定输入矩阵

∈

X in mathbb{R}^{n times m}

$X \in R^{n \times m}$ ，其中

$n$ 是样本数，

$m$ 是特征数，给定输入的类簇中心

∈

y in mathbb{R}^m

$y \in R^{m}$ 。

我们要计算

$n$ 个样本到某一类簇中心

$y$ 的欧式距离，最后的结果是

∈

E in mathbb{R}^{n}

$E \in R^{n}$ ，每个元素表示矩阵

$X$ 中的每个样本到类中心

$y$ 的欧式距离。

def compute_distance(X, y):
    '''
    计算样本矩阵X与类中心y之间的欧氏距离
    
    Parameters
    ----------
    X, np.ndarray, 样本矩阵 X, 维度：(n, m)
    
    y, np.ndarray, 类中心 y，维度：(m, )
    
    Returns
    ----------
    distance, np.ndarray, 样本矩阵 X 每个样本到类中心 y 之间的欧式距离，维度：(n, )
    '''
    
    # YOUR CODE HERE
    y= np.tile(y, (X.shape[0], 1))
    distance = np.sum(((X-y)**2),axis=1)**0.5
    return distance

# 测试样例
print(compute_distance(np.array([[0, 0], [0, 1]]), np.array([0, 1]))) # [ 1.  0.]
print(compute_distance(np.array([[0, 0], [0, 1]]), np.array([1, 1]))) # [ 1.41421356  1.        ]

下面开始实现K-means聚类算法

class myKmeans:
    def __init__(self, n_clusters, max_iter = 100):
        '''
        初始化，三个成员变量
        
        Parameters
        ----------
        n_clusters: int, 类簇的个数
        
        max_iter, int, default 100, 最大迭代轮数，默认为100
        
        '''
        # 表示类簇的个数
        self.n_clusters = n_clusters
        
        # 表示最大迭代次数
        self.max_iter = int(max_iter)
        
        # 类簇中心
        self.centroids = None
    
    def choose_centroid(self, X):
        '''
        选取类簇中心
        
        Parameters
        ----------
        X: np.ndarray, 样本矩阵X，维度：(n, m)
        
        Returns
        ----------
        centroids: np.ndarray, 维度：(n_clusters, m)
        
        '''
        centroids = X[np.random.choice(np.arange(len(X)), self.n_clusters, replace = False), :]
        return centroids
    
    def compute_label(self, X):
        '''
        给定样本矩阵X，结合类中心矩阵self.centroids，计算样本矩阵X内每个样本属于哪个类簇
        
        Parameters
        ----------
        X: np.ndarray, 样本矩阵X，维度：(n, m)
        
        Returns
        ----------
        labels: np.ndarray, 维度：(n, )
        
        '''
        # 将每个样本到每个类簇中心的距离存储在distances中，每行表示当前样本对于不同的类中心的距离
        distances = np.empty((len(X), self.n_clusters))
        
        # 遍历类中心，对每个类中心，计算所有的样本到这个类中心的距离
        for index in range(len(self.centroids)):
            
            # 计算样本矩阵X所有样本到当前类中心的距离，存储在distances中的第index列中
            # YOUR CODE HERE
            distances[:, index] = compute_distance(X, self.centroids[index])
            
        # 取distances每行最小值的下标，这个下标就是这个样本属于的类簇的标记
        # YOUR CODE HERE
        labels = np.argmin(distances, axis=1)
        
        # 返回每个样本属于的类簇的标记
        return labels
    
    def fit(self, X):
        '''
        聚类，包含类中心初始化，类中心优化两个部分
        
        Parameters
        ----------
        X: np.ndarray, 样本矩阵X，维度：(n, m)
        
        '''
        # 类中心随机初始化
        self.centroids = self.choose_centroid(X)
        
        # 优化self.max_iter轮
        for epoch in range(self.max_iter):
            
            # 计算当前所有样本的属于哪个类簇
            labels = self.compute_label(X)
            
            # 重新计算每个类簇的类中心
            for index in range(self.n_clusters):
                
                # 重新计算第 index 个类中心，对属于这个类簇的样本取均值
                # YOUR CODE HERE
                self.centroids[index, :] = X[labels == index].sum(axis=0) / X[labels == index].shape[0]

4. 聚类

# 初始化一个3类簇的模型
model = myKmeans(3)

# 对X进行聚类，计算类中心
model.fit(X)

# 计算X的类标记
prediction = model.compute_label(X)

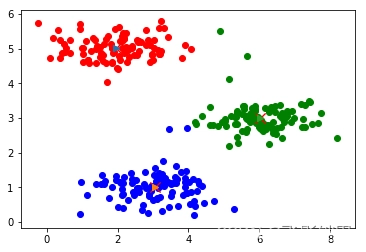
5. 聚类结果可视化

# 使用我们的预测结果上色
plt.scatter(X[:, 0], X[:, 1], c = prediction)

6. 评价指标

这里，我们选用两个外部指标，FMI和NMI。

from sklearn.metrics import normalized_mutual_info_score
from sklearn.metrics import fowlkes_mallows_score
print(normalized_mutual_info_score(y, prediction))
print(fowlkes_mallows_score(y, prediction))

Test

使用下面提供的数据，完成以下实验：

使用myKmeans和层次聚类算法(AgglomerativeClustering)对该数据进行聚类。
计算出两个模型的FMI和NMI值，并对聚类结果可视化。
分析为什么两个模型的聚类效果会出现如此的不同。

要求：

层次聚类的连接方式选择’single’，即使用两个类簇之间的最小距离
类簇个数设定为2

完成下表的填写：

双击此处填写

算法	FMI	NMI
myKmeans	0.4996	0.0003
AgglomerativeClustering	1.0000	1.0000

from sklearn.datasets import make_circles
X, y = make_circles(n_samples = 1500, factor = .5, noise = .05, random_state = 32)
plt.scatter(X[:, 0], X[:, 1], c = y)

# 初始化一个2类簇的模型
model_test = myKmeans(2)

# 对X进行聚类，计算类中心
model_test.fit(X)

# 计算X的类标记
prediction = model_test.compute_label(X)
plt.figure(figsize=(12, 4))

plt.subplot(1, 2, 1)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis', s=40)
plt.title("True Clusters")

plt.subplot(1, 2, 2)
plt.scatter(X[:, 0], X[:, 1], c=prediction, cmap='viridis', s=40)
plt.title("Agglomerative Clustering")

plt.show()

# 计算评估指标
fmi1 = fowlkes_mallows_score(y, prediction)
nmi1 = normalized_mutual_info_score(y, prediction)
print(f"K-means - Fowlkes Mallows Index: {fmi1:.4f}")
print(f"K-means - Normalized Mutual Info: {nmi1:.4f}")

# YOUR CODE HERE
agg2 = AgglomerativeClustering(n_clusters=2, linkage='single')
labels2 = agg2.fit_predict(X)
plt.figure(figsize=(12, 4))

plt.subplot(1, 2, 1)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis', s=40)
plt.title("True Clusters")

plt.subplot(1, 2, 2)
plt.scatter(X[:, 0], X[:, 1], c=labels2, cmap='viridis', s=40)
plt.title("Agglomerative Clustering")

plt.show()

# 计算评估指标
fmi2 = fowlkes_mallows_score(y, labels2)
nmi2 = normalized_mutual_info_score(y, labels2)
print(f"层次聚类 - Fowlkes Mallows Index: {nmi2:.4f}")
print(f"层次聚类 - Normalized Mutual Info: {nmi2:.4f}")