面试算法105：最大的岛屿

本文介绍: 海洋岛屿地图可以用由0、1组成的二维数组表示，水平或竖直方向相连的一组1表示一个岛屿，请计算最大的岛屿的面积（即岛屿中1的数目）。例如，在下图中有4个岛屿，其中最大的岛屿的面积为5。

题目

海洋岛屿地图可以用由0、1组成的二维数组表示，水平或竖直方向相连的一组1表示一个岛屿，请计算最大的岛屿的面积（即岛屿中1的数目）。例如，在下图中有4个岛屿，其中最大的岛屿的面积为5。
在这里插入图片描述

分析

将岛屿转换成图之后，岛屿的面积就变成子图中节点的数目。如果能计算出每个连通子图中节点的数目，就能知道最大的岛屿的面积。
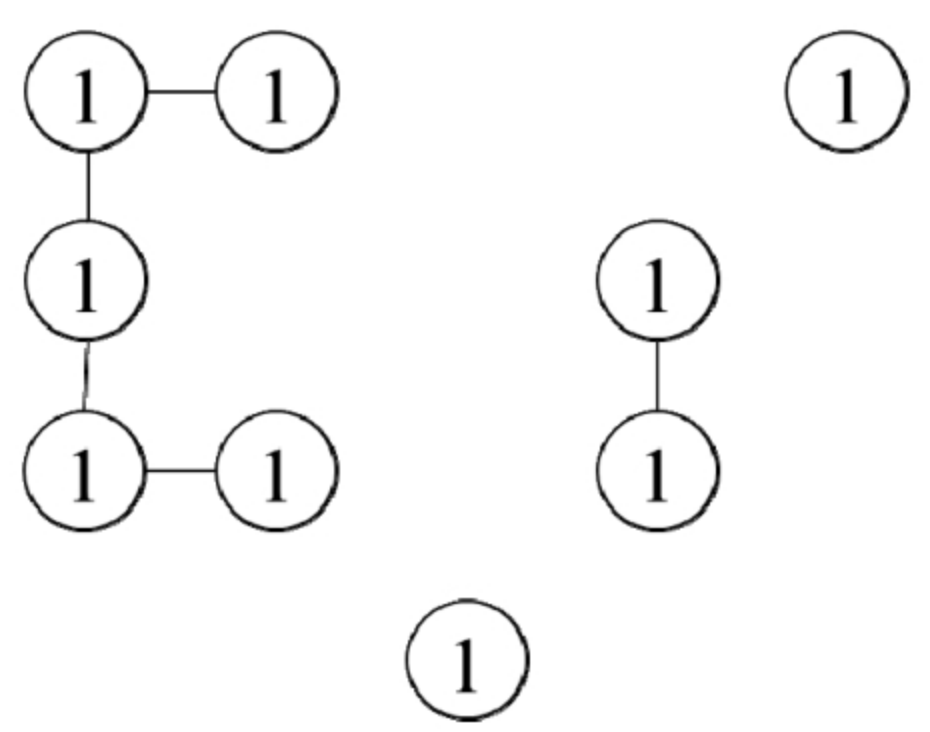
在这里插入图片描述
可以逐一扫描矩阵中的每个格子，如果遇到一个值为1的格子并且它不在之前已知的岛屿上，那么就到达了一个新的岛屿，于是搜索这个岛屿并计算它的面积。在比较所有岛屿的面积之后就可以知道最大的岛屿的面积。
二维数组dirs表示在矩阵中向上、下、左、右这4个方向前进一步时坐标的变化。在矩阵中向上移动一步时行号减1而列号不变，所以坐标的改变值为（-1，0），其他方向的改变值类似。用当前坐标pos加上坐标的改变值就得到向不同方向前进一步之后的坐标。这样写代码的好处是容易用一个简洁的循环实现向4个不同方向前进。

解：广度优先搜索

public class Test {
    public static void main(String[] args) {
        int[][] grid = {
            {1, 1, 0, 0, 1},
            {1, 0, 0, 1, 0},
            {1, 1, 0, 1, 0},
            {0, 0, 1, 0, 0},
        };
        int result = maxAreaOfIsland(grid);
        System.out.println(result);
    }

    public static int maxAreaOfIsland(int[][] grid) {
        int rows = grid.length;
        int cols = grid[0].length;
        boolean[][] visited = new boolean[rows][cols];
        int maxArea = 0;
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                if (grid[i][j] == 1 && !visited[i][j]) {
                    int area = getArea(grid, visited, i, j);
                    maxArea = Math.max(maxArea, area);
                }
            }
        }

        return maxArea;
    }

    // 广度优先搜索
    private static int getArea(int[][] grid, boolean[][] visited, int i, int j) {
        Queue<int[]> queue = new LinkedList<>();
        queue.add(new int[] {i, j});
        visited[i][j] = true;

        int[][] dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
        int area = 0;
        while (!queue.isEmpty()) {
            int[] pos = queue.remove();
            area++;

            for (int[] dir : dirs) {
                int r = pos[0] + dir[0];
                int c = pos[1] + dir[1];
                if (r >= 0 && r < grid.length && c >= 0 && c < grid[0].length && grid[r][c] == 1 && !visited[r][c]) {
                    queue.add(new int[] {r, c});
                    visited[r][c] = true;
                }
            }
        }

        return area;
    }

}

解：基于栈实现深度优先搜索

public class Test {
    public static void main(String[] args) {
        int[][] grid = {
            {1, 1, 0, 0, 1},
            {1, 0, 0, 1, 0},
            {1, 1, 0, 1, 0},
            {0, 0, 1, 0, 0},
        };
        int result = maxAreaOfIsland(grid);
        System.out.println(result);
    }

    public static int maxAreaOfIsland(int[][] grid) {
        int rows = grid.length;
        int cols = grid[0].length;
        boolean[][] visited = new boolean[rows][cols];
        int maxArea = 0;
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                if (grid[i][j] == 1 && !visited[i][j]) {
                    int area = getArea(grid, visited, i, j);
                    maxArea = Math.max(maxArea, area);
                }
            }
        }

        return maxArea;
    }

    // 基于栈实现深度优先搜索
    private static int getArea(int[][] grid, boolean[][] visited, int i, int j) {
        Stack<int[]> stack = new Stack<>();
        stack.push(new int[] {i, j});
        visited[i][j] = true;

        int[][] dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
        int area = 0;
        while (!stack.isEmpty()) {
            int[] pos = stack.pop();
            area++;

            for (int[] dir : dirs) {
                int r = pos[0] + dir[0];
                int c = pos[1] + dir[1];
                if (r >= 0 && r < grid.length && c >= 0 && c < grid[0].length && grid[r][c] == 1 && !visited[r][c]) {
                    stack.push(new int[] {r, c});
                    visited[r][c] = true;
                }
            }
        }

        return area;
    }

}

解：基于递归实现深度优先搜索

public class Test {
    public static void main(String[] args) {
        int[][] grid = {
            {1, 1, 0, 0, 1},
            {1, 0, 0, 1, 0},
            {1, 1, 0, 1, 0},
            {0, 0, 1, 0, 0},
        };
        int result = maxAreaOfIsland(grid);
        System.out.println(result);
    }

    public static int maxAreaOfIsland(int[][] grid) {
        int rows = grid.length;
        int cols = grid[0].length;
        boolean[][] visited = new boolean[rows][cols];
        int maxArea = 0;
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                if (grid[i][j] == 1 && !visited[i][j]) {
                    int area = getArea(grid, visited, i, j);
                    maxArea = Math.max(maxArea, area);
                }
            }
        }

        return maxArea;
    }

    // 基于递归实现深度优先搜索
    private static int getArea(int[][] grid, boolean[][] visited, int i, int j) {
        int area = 1;
        visited[i][j] = true;
        int[][] dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
        for (int[] dir : dirs) {
            int r = i + dir[0];
            int c = j + dir[1];
            if (r >= 0 && r < grid.length && c >= 0 && c < grid[0].length && grid[r][c] == 1 && !visited[r][c]) {
                area += getArea(grid, visited, r, c);
            }
        }

        return area;
    }

}