本文介绍: 数组、矩阵
一、数组
数组的特点:
数组数目固定,一旦定义了数组结构,不再有元素个数的增减变化。因此,数组一般不做插入、删除操作,适合用于顺序存储结构。
1-1、一维数组

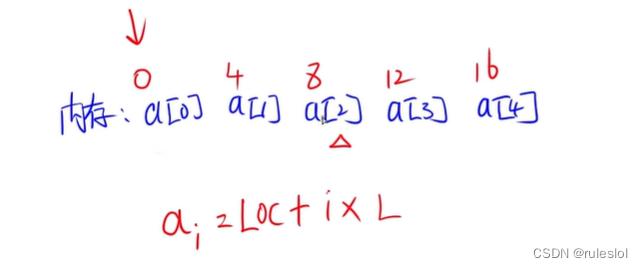
数组从0开始:
ai的地址 = LOC + (i)*L
1-2、二维数组
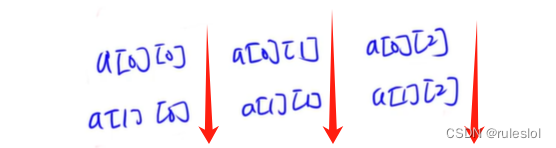
1、a[N][M]按行优先存储
2、a[N][M]按列优先存储
3、特殊情况a[N][N]
1-3、真题
二、矩阵
2-1、特殊矩阵
2-1-1、对称矩阵
2-1-2、三对角矩阵
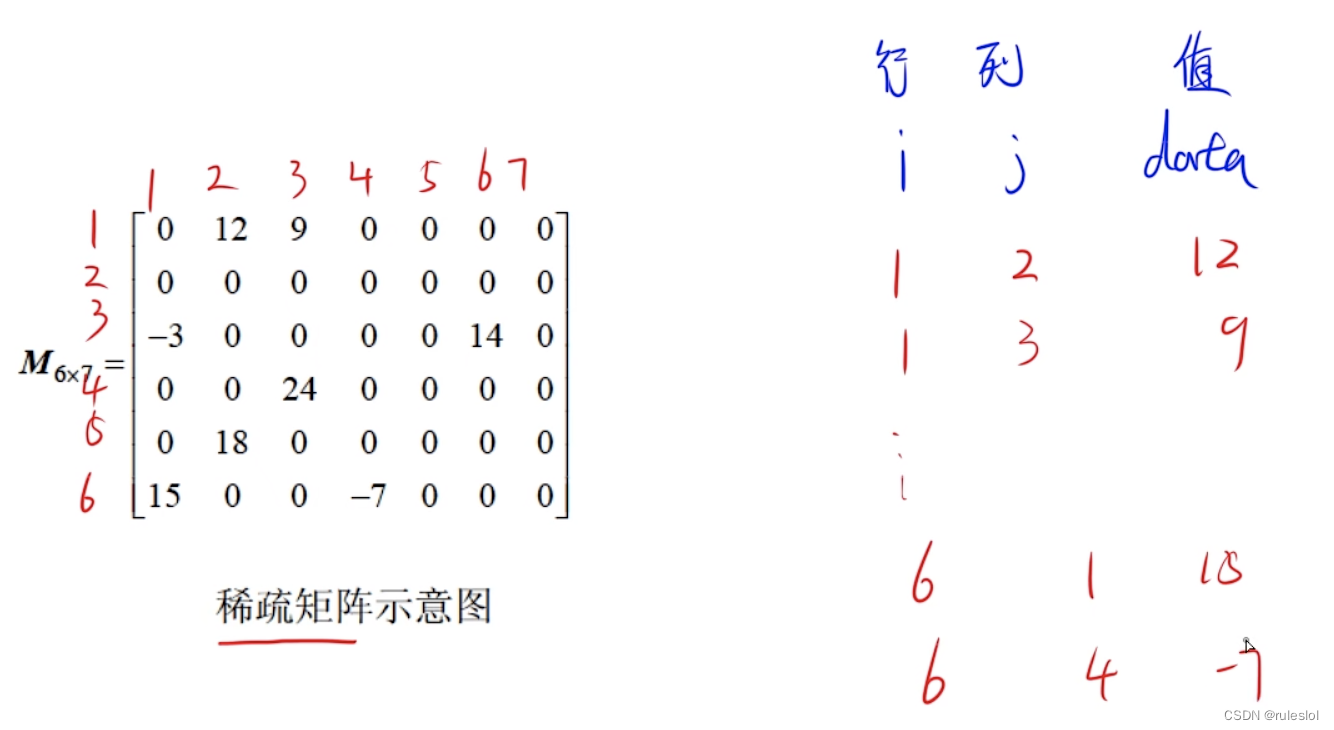
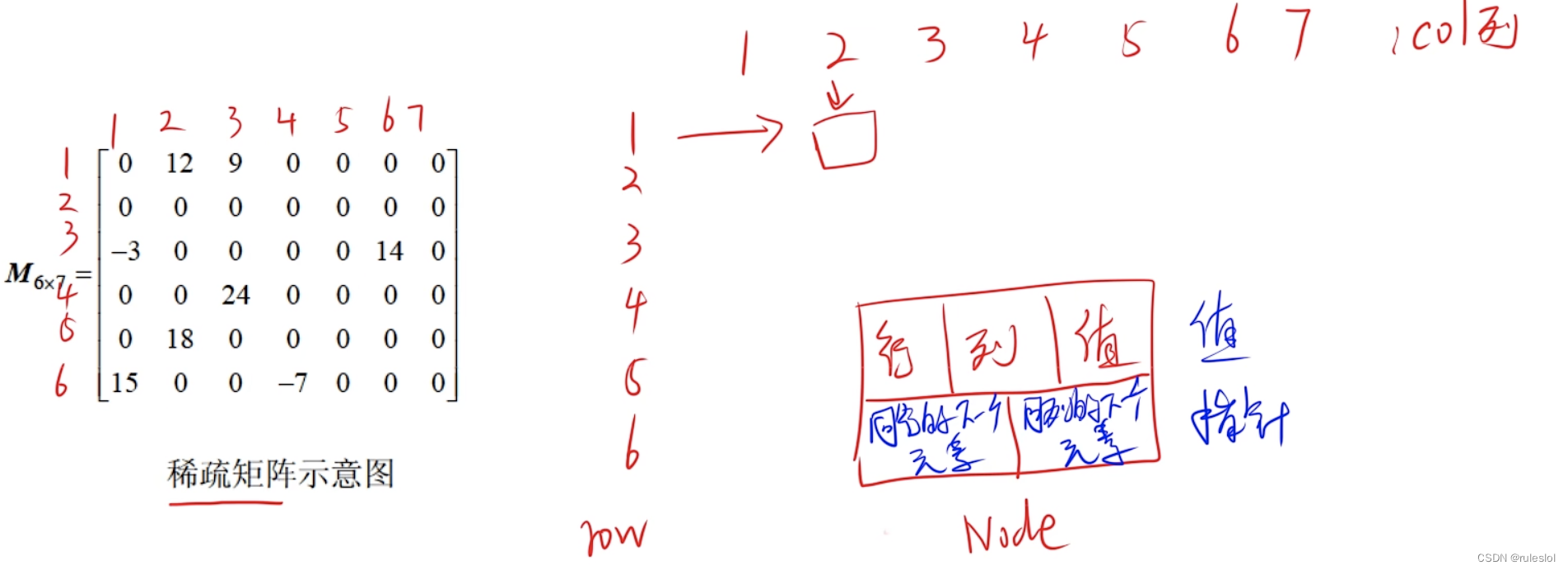
2-2、稀疏矩阵
2-2-3、三元组顺序表
2-2-4、十字链表
2-3、真题
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。






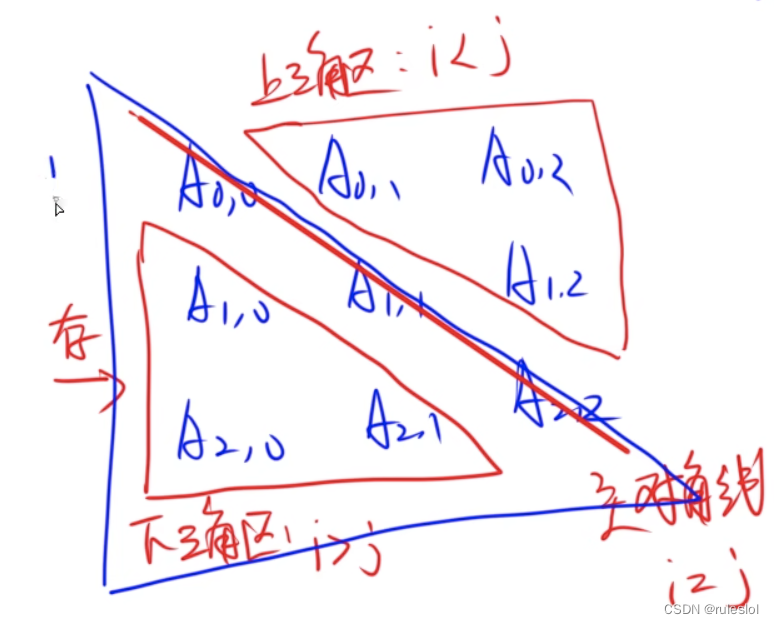
 真题3:
真题3:















 真题7:
真题7: