本文介绍: 本节课程思维导图:我们今天讲另外一种特殊的树,“堆”(Heap)。堆这种数据结构的应用场景非常多,最经典的莫过于堆排序了。堆排序是一种原地的、时间复杂度为 O(nlogn) 的排序算法。快速排序和堆排序这两种排序算法的时间复杂度都是 O(nlogn),甚至堆排序比快速排序的时间复杂度还要稳定,但是,在实际的软件开发中,快速排序的性能要比堆排序好,这是为什么呢?
前言

本节课程思维导图:
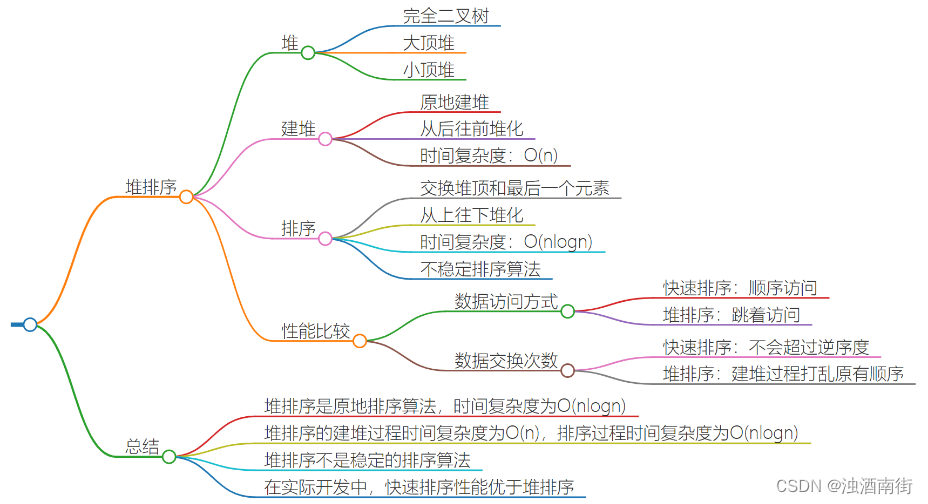
我们今天讲另外一种特殊的树,“堆”(Heap)。堆这种数据结构的应用场景非常多,最经典的莫过于堆排序了。堆排序是一种原地的、时间复杂度为 O(nlogn) 的排序算法。
快速排序和堆排序这两种排序算法的时间复杂度都是 O(nlogn),甚至堆排序比快速排序的时间复杂度还要稳定,但是,在实际的软件开发中,快速排序的性能要比堆排序好,这是为什么呢?
如何理解“堆”?
我们现在就来看看,什么样的树才是堆。我罗列了两点要求,只要满足这两点,它就是一个堆。
第一点,堆必须是一个完全二叉树。完全二叉树要求,除了最后一层,其他层的节点个数都是满的,最后一层的节点都靠左排列。
第二点,堆中的每个节点的值必须大于等于(或者小于等于)其子树中每个节点的值。实际上,我们还可以换一种说法,堆中每个节点的值都大于等于(或者小于等于)其左右子节点的值。这两种表述是等价的。
对于每个节点的值都大于等于子树中每个节点值的堆,我们叫做“大顶堆”。对于每个节点的值都小于等于子树中每个节点值的堆,我们叫做“小顶堆”。
如何实现一个堆?
要实现一个堆,我们先要知道,堆都支持哪些操作以及如何存储一个堆。
完全二叉树比较适合用数组来存储。用数组来存储完全二叉树是非常节省存储空间的。
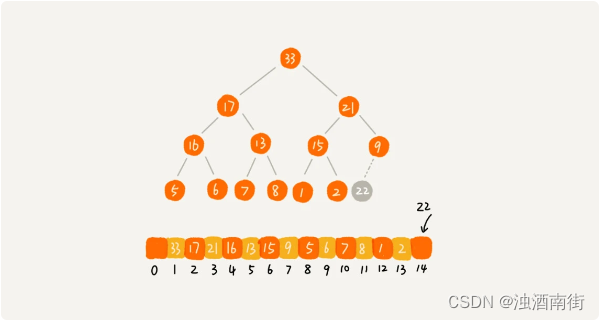
假设,堆中的数据是从数组下标为 1 的位置开始存储,我们来看一个用数组存储堆的例子。
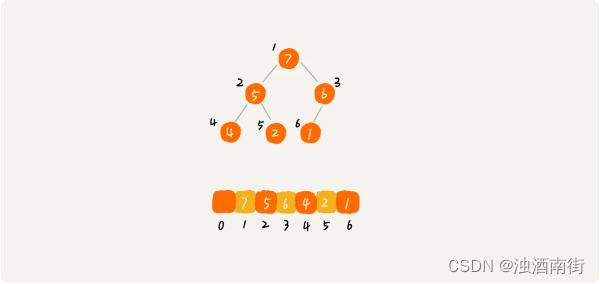
从图中我们可以看到,数组中下标为 i 的节点的左子节点,就是下标为 i∗2 的节点,右子节点就是下标为 i∗2+1 的节点,父节点就是下标为 i∗1/2的节点。
知道了如何存储一个堆,那我们再来看看,堆上的操作有哪些呢?我罗列了几个非常核心的操作,分别是往堆中插入一个元素和删除堆顶元素。
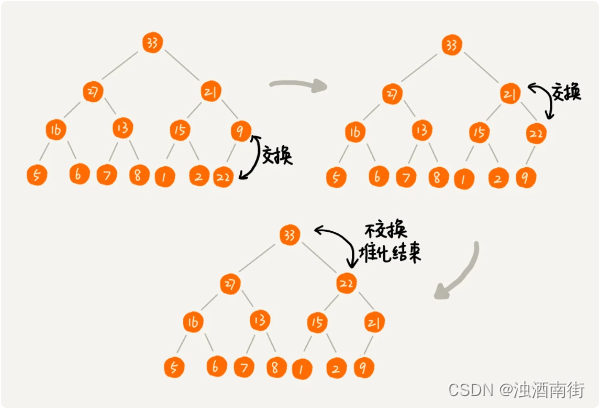
1. 往堆中插入一个元素
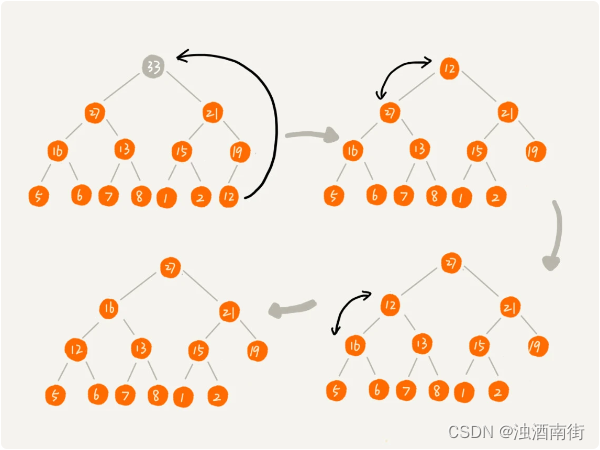
2. 删除堆顶元素
如何基于堆实现排序?
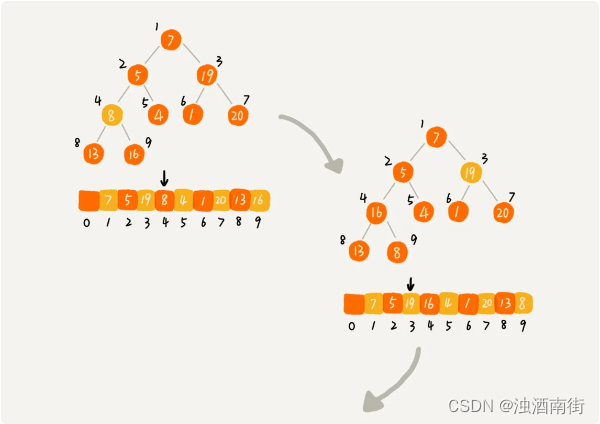
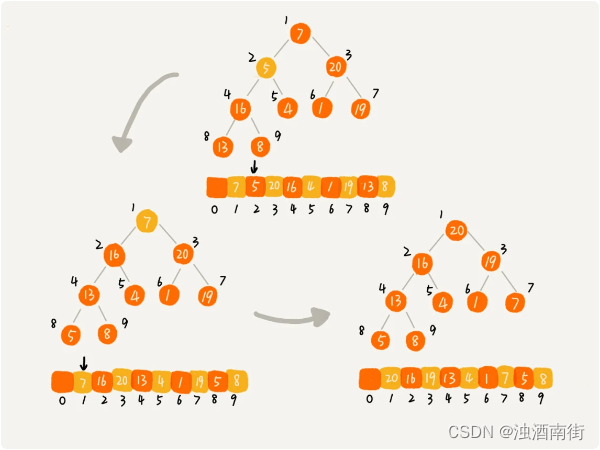
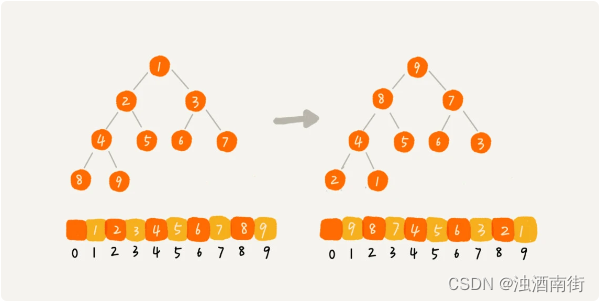
1. 建堆
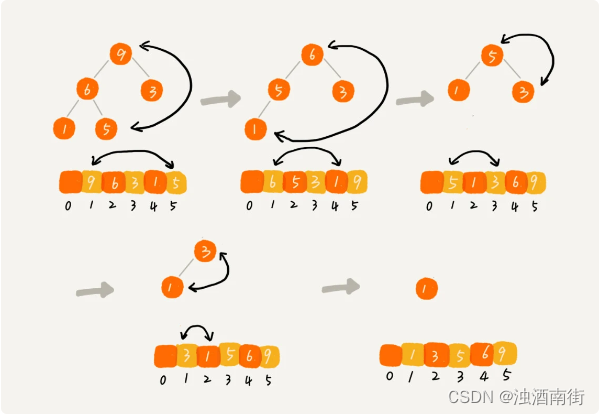
2. 排序
解答开篇
内容小结
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。