基于C#实现Kruskal算法

这篇我们看看第二种生成树的 Kruskal 算法，这个算法的魅力在于我们可以打一下算法和数据结构的组合拳，很有意思的。

一、思想

若存在 M={0,1,2,3,4,5}这样 6 个节点，我们知道 Prim 算法构建生成树是从”顶点”这个角度来思考的，然后采用“贪心思想”来一步步扩大化，最后形成整体最优解，而 Kruskal 算法有点意思，它是站在”边“这个角度在思考的，首先我有两个集合。

1.1、顶点集合(vertexs)

比如 M 集合中的每个元素都可以认为是一个独根树（是不是想到了并查集？）。

1.2、边集合(edges)

对图中的每条边按照权值大小进行排序。（是不是想到了优先队列？）
首先：我们从 edges 中选出权值最小的一条边来作为生成树的一条边，然后将该边的两个顶点合并为一个新的树。
然后：我们继续从 edges 中选出次小的边作为生成树的第二条边，但是前提就是边的两个顶点一定是属于两个集合中，如果不是则剔除该边继续选下一条次小边。
最后：经过反复操作，当我们发现 n 个顶点的图中生成树已经有 n-1 边的时候，此时生成树构建完毕。


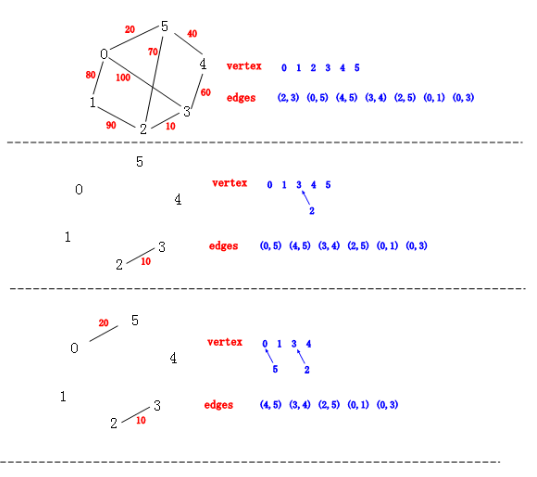
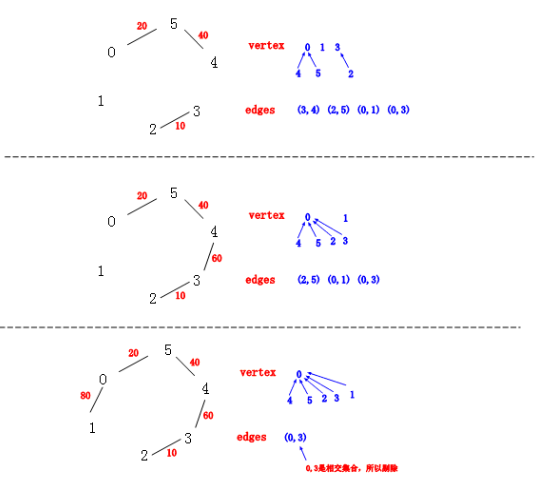
从图中我们还是很清楚的看到 Kruskal 算法构建生成树的详细过程，同时我们也看到了”并查集“和“优先队列“这两个神器来加速我们的生成树构建。

二、构建

2.1、Build 方法

这里我灌的是一些测试数据，同时在矩阵构建完毕后，将顶点信息放入并查集，同时将边的信息放入优先队列，方便我们在做生成树的时候秒杀。

 #region 矩阵的构建
 /// <summary>
 /// 矩阵的构建
 /// </summary&gt;
 public void Build()
 {
     //顶点数
     graph.vertexsNum = 6;

     //边数
     graph.edgesNum = 8;

     graph.vertexs = new int[graph.vertexsNum];

     graph.edges = new int[graph.vertexsNum, graph.vertexsNum];

     //构建二维数组
     for (int i = 0; i < graph.vertexsNum; i++)
     {
         //顶点
         graph.vertexs[i] = i;

         for (int j = 0; j < graph.vertexsNum; j++)
         {
             graph.edges[i, j] = int.MaxValue;
         }
     }

     graph.edges[0, 1] = graph.edges[1, 0] = 80;
     graph.edges[0, 3] = graph.edges[3, 0] = 100;
     graph.edges[0, 5] = graph.edges[5, 0] = 20;
     graph.edges[1, 2] = graph.edges[2, 1] = 90;
     graph.edges[2, 5] = graph.edges[5, 2] = 70;
     graph.edges[4, 5] = graph.edges[5, 4] = 40;
     graph.edges[3, 4] = graph.edges[4, 3] = 60;
     graph.edges[2, 3] = graph.edges[3, 2] = 10;

     //优先队列，存放树中的边
     queue = new PriorityQueue<Edge>();

     //并查集
     set = new DisjointSet<int>(graph.vertexs);

     //将对角线读入到优先队列
     for (int i = 0; i < graph.vertexsNum; i++)
     {
         for (int j = i; j < graph.vertexsNum; j++)
         {
             //说明该边有权重
             if (graph.edges[i, j] != int.MaxValue)
             {
                 queue.Eequeue(new Edge()
                 {
                     startEdge = i,
                     endEdge = j,
                     weight = graph.edges[i, j]
                 }, graph.edges[i, j]);
             }
         }
     }
 }
 #endregion

2.2、Kruskal 算法

并查集，优先队列都有数据了，下面我们只要出队操作就行了，如果边的顶点不在一个集合中，我们将其收集作为最小生成树的一条边，按着这样的方式，最终生成树构建完毕。

 #region Kruskal算法
 /// <summary>
 /// Kruskal算法
 /// </summary>
 public List<Edge> Kruskal()
 {
     //最后收集到的最小生成树的边
     List<Edge> list = new List<Edge>();

     //循环队列
     while (queue.Count() > 0)
     {
         var edge = queue.Dequeue();

         //如果该两点是同一个集合，则剔除该集合
         if (set.IsSameSet(edge.t.startEdge, edge.t.endEdge))
             continue;

         list.Add(edge.t);

         //然后将startEdge 和 endEdge Union起来，表示一个集合
         set.Union(edge.t.startEdge, edge.t.endEdge);

         //如果n个节点有n-1边的时候，此时生成树已经构建完毕，提前退出
         if (list.Count == graph.vertexsNum - 1)
             break;
     }

     return list;
 }
 #endregion

最后是总的代码：

 using System;
 using System.Collections.Generic;
 using System.Linq;
 using System.Text;
 using System.Diagnostics;
 using System.Threading;
 using System.IO;
 using System.Threading.Tasks;
 
 namespace ConsoleApplication2
 {
     public class Program
     {
         public static void Main()
         {
             MatrixGraph graph = new MatrixGraph();
 
             graph.Build();
 
             var edges = graph.Kruskal();
 
             foreach (var edge in edges)
             {
                 Console.WriteLine("({0},{1})({2})", edge.startEdge, edge.endEdge, edge.weight);
             }
 
             Console.Read();
         }
     }
 
     #region 定义矩阵节点
     /// <summary>
     /// 定义矩阵节点
     /// </summary>
     public class MatrixGraph
     {
         Graph graph = new Graph();
 
         PriorityQueue<Edge> queue;
 
         DisjointSet<int> set;
 
         public class Graph
         {
             /// <summary>
             /// 顶点信息
             /// </summary>
             public int[] vertexs;
 
             /// <summary>
             /// 边的条数
             /// </summary>
             public int[,] edges;
 
             /// <summary>
             /// 顶点个数
             /// </summary>
             public int vertexsNum;
 
             /// <summary>
             /// 边的个数
             /// </summary>
             public int edgesNum;
         }
 
         #region 矩阵的构建
         /// <summary>
         /// 矩阵的构建
         /// </summary>
         public void Build()
         {
             //顶点数
             graph.vertexsNum = 6;
 
             //边数
             graph.edgesNum = 8;
 
             graph.vertexs = new int[graph.vertexsNum];
 
             graph.edges = new int[graph.vertexsNum, graph.vertexsNum];
 
             //构建二维数组
             for (int i = 0; i < graph.vertexsNum; i++)
             {
                 //顶点
                 graph.vertexs[i] = i;
 
                 for (int j = 0; j < graph.vertexsNum; j++)
                 {
                     graph.edges[i, j] = int.MaxValue;
                 }
             }
 
             graph.edges[0, 1] = graph.edges[1, 0] = 80;
             graph.edges[0, 3] = graph.edges[3, 0] = 100;
             graph.edges[0, 5] = graph.edges[5, 0] = 20;
             graph.edges[1, 2] = graph.edges[2, 1] = 90;
             graph.edges[2, 5] = graph.edges[5, 2] = 70;
             graph.edges[4, 5] = graph.edges[5, 4] = 40;
             graph.edges[3, 4] = graph.edges[4, 3] = 60;
             graph.edges[2, 3] = graph.edges[3, 2] = 10;

             //优先队列，存放树中的边
             queue = new PriorityQueue<Edge>();
 
             //并查集
             set = new DisjointSet<int>(graph.vertexs);
 
             //将对角线读入到优先队列
             for (int i = 0; i < graph.vertexsNum; i++)
             {
                 for (int j = i; j < graph.vertexsNum; j++)
                 {
                     //说明该边有权重
                     if (graph.edges[i, j] != int.MaxValue)
                     {
                         queue.Eequeue(new Edge()
                         {
                             startEdge = i,
                             endEdge = j,
                             weight = graph.edges[i, j]
                         }, graph.edges[i, j]);
                     }
                 }
             }
         }
         #endregion
 
         #region 边的信息
         /// <summary>
         /// 边的信息
         /// </summary>
         public class Edge
         {
             //开始边
             public int startEdge;
 
             //结束边
             public int endEdge;
 
             //权重
             public int weight;
         }
         #endregion
 
         #region Kruskal算法
         /// <summary>
         /// Kruskal算法
         /// </summary>
         public List<Edge> Kruskal()
         {
             //最后收集到的最小生成树的边
             List<Edge> list = new List<Edge>();
 
             //循环队列
             while (queue.Count() > 0)
             {
                 var edge = queue.Dequeue();
 
                 //如果该两点是同一个集合，则剔除该集合
                 if (set.IsSameSet(edge.t.startEdge, edge.t.endEdge))
                     continue;
 
                 list.Add(edge.t);
 
                 //然后将startEdge 和 endEdge Union起来，表示一个集合
                 set.Union(edge.t.startEdge, edge.t.endEdge);
 
                 //如果n个节点有n-1边的时候，此时生成树已经构建完毕，提前退出
                 if (list.Count == graph.vertexsNum - 1)
                     break;
             }
 
             return list;
         }
         #endregion
     }
     #endregion
 }

并查集：

 using System;
 using System.Collections.Generic;
 using System.Linq;
 using System.Text;
 
 namespace ConsoleApplication2
 {
     /// <summary>
     /// 并查集
     /// </summary>
     public class DisjointSet<T> where T : IComparable
     {
         #region 树节点
         /// <summary>
         /// 树节点
         /// </summary>
         public class Node
         {
             /// <summary>
             /// 父节点
             /// </summary>
             public T parent;
 
             /// <summary>
             /// 节点的秩
             /// </summary>
             public int rank;
         }
         #endregion
 
         Dictionary<T, Node> dic = new Dictionary<T, Node>();
 
         public DisjointSet(T[] c)
         {
             Init(c);
         }
 
         #region 做单一集合的初始化操作
         /// <summary>
         /// 做单一集合的初始化操作
         /// </summary>
         public void Init(T[] c)
         {
             //默认的不想交集合的父节点指向自己
             for (int i = 0; i < c.Length; i++)
             {
                 dic.Add(c[i], new Node()
                 {
                     parent = c[i],
                     rank = 0
                 });
             }
         }
         #endregion
 
         #region 判断两元素是否属于同一个集合
         /// <summary>
         /// 判断两元素是否属于同一个集合
         /// </summary>
         /// <param name="root1"></param>
         /// <param name="root2"></param>
         /// <returns></returns>
         public bool IsSameSet(T root1, T root2)
         {
             return Find(root1).CompareTo(Find(root2)) == 0;
         }
         #endregion
 
         #region  查找x所属的集合
         /// <summary>
         /// 查找x所属的集合
         /// </summary>
         /// <param name="x"></param>
         /// <returns></returns>
         public T Find(T x)
         {
             //如果相等，则说明已经到根节点了，返回根节点元素
             if (dic[x].parent.CompareTo(x) == 0)
                 return x;
 
             //路径压缩(回溯的时候赋值，最终的值就是上面返回的"x"，也就是一条路径上全部被修改了)
             return dic[x].parent = Find(dic[x].parent);
         }
         #endregion
 
         #region 合并两个不相交集合
         /// <summary>
         /// 合并两个不相交集合
         /// </summary>
         /// <param name="root1"></param>
         /// <param name="root2"></param>
         /// <returns></returns>
         public void Union(T root1, T root2)
         {
             T x1 = Find(root1);
             T y1 = Find(root2);
 
             //如果根节点相同则说明是同一个集合
             if (x1.CompareTo(y1) == 0)
                 return;
 
             //说明左集合的深度 < 右集合
             if (dic[x1].rank < dic[y1].rank)
             {
                 //将左集合指向右集合
                 dic[x1].parent = y1;
             }
             else
             {
                 //如果 秩 相等，则将 y1 并入到 x1 中，并将x1++
                 if (dic[x1].rank == dic[y1].rank)
                     dic[x1].rank++;
 
                 dic[y1].parent = x1;
             }
         }
         #endregion
     }
 }

优先队列：

 using System;
 using System.Collections.Generic;
 using System.Linq;
 using System.Text;
 using System.Diagnostics;
 using System.Threading;
 using System.IO;
 
 namespace ConsoleApplication2
 {
     public class PriorityQueue<T> where T : class
     {
         /// <summary>
         /// 定义一个数组来存放节点
         /// </summary>
         private List<HeapNode> nodeList = new List<HeapNode>();
 
         #region 堆节点定义
         /// <summary>
         /// 堆节点定义
         /// </summary>
         public class HeapNode
         {
             /// <summary>
             /// 实体数据
             /// </summary>
             public T t { get; set; }
 
             /// <summary>
             /// 优先级别 1-10个级别 (优先级别递增)
             /// </summary>
             public int level { get; set; }
 
             public HeapNode(T t, int level)
             {
                 this.t = t;
                 this.level = level;
             }
 
             public HeapNode() { }
         }
         #endregion
 
         #region  添加操作
         /// <summary>
         /// 添加操作
         /// </summary>
         public void Eequeue(T t, int level = 1)
         {
             //将当前节点追加到堆尾
             nodeList.Add(new HeapNode(t, level));
 
             //如果只有一个节点，则不需要进行筛操作
             if (nodeList.Count == 1)
                 return;
 
             //获取最后一个非叶子节点
             int parent = nodeList.Count / 2 - 1;
 
             //堆调整
             UpHeapAdjust(nodeList, parent);
         }
         #endregion
 
         #region 对堆进行上滤操作，使得满足堆性质
         /// <summary>
         /// 对堆进行上滤操作，使得满足堆性质
         /// </summary>
         /// <param name="nodeList"></param>
         /// <param name="index">非叶子节点的之后指针（这里要注意：我们
         /// 的筛操作时针对非叶节点的）
         /// </param>
         public void UpHeapAdjust(List<HeapNode> nodeList, int parent)
         {
             while (parent >= 0)
             {
                 //当前index节点的左孩子
                 var left = 2 * parent + 1;
 
                 //当前index节点的右孩子
                 var right = left + 1;
 
                 //parent子节点中最大的孩子节点，方便于parent进行比较
                 //默认为left节点
                 var min = left;
 
                 //判断当前节点是否有右孩子
                 if (right < nodeList.Count)
                 {
                     //判断parent要比较的最大子节点
                     min = nodeList[left].level < nodeList[right].level ? left : right;
                 }
 
                 //如果parent节点大于它的某个子节点的话，此时筛操作
                 if (nodeList[parent].level > nodeList[min].level)
                 {
                     //子节点和父节点进行交换操作
                     var temp = nodeList[parent];
                     nodeList[parent] = nodeList[min];
                     nodeList[min] = temp;
 
                     //继续进行更上一层的过滤
                     parent = (int)Math.Ceiling(parent / 2d) - 1;
                 }
                 else
                 {
                     break;
                 }
             }
         }
         #endregion
 
         #region 优先队列的出队操作
         /// <summary>
         /// 优先队列的出队操作
         /// </summary>
         /// <returns></returns>
         public HeapNode Dequeue()
         {
             if (nodeList.Count == 0)
                 return null;
 
             //出队列操作，弹出数据头元素
             var pop = nodeList[0];
 
             //用尾元素填充头元素
             nodeList[0] = nodeList[nodeList.Count - 1];
 
             //删除尾节点
             nodeList.RemoveAt(nodeList.Count - 1);
 
             //然后从根节点下滤堆
             DownHeapAdjust(nodeList, 0);
 
             return pop;
         }
         #endregion
 
         #region  对堆进行下滤操作，使得满足堆性质
         /// <summary>
         /// 对堆进行下滤操作，使得满足堆性质
         /// </summary>
         /// <param name="nodeList"></param>
         /// <param name="index">非叶子节点的之后指针（这里要注意：我们
         /// 的筛操作时针对非叶节点的）
         /// </param>
         public void DownHeapAdjust(List<HeapNode> nodeList, int parent)
         {
             while (2 * parent + 1 < nodeList.Count)
             {
                 //当前index节点的左孩子
                 var left = 2 * parent + 1;
 
                 //当前index节点的右孩子
                 var right = left + 1;
 
                 //parent子节点中最大的孩子节点，方便于parent进行比较
                 //默认为left节点
                 var min = left;
 
                 //判断当前节点是否有右孩子
                 if (right < nodeList.Count)
                 {
                     //判断parent要比较的最大子节点
                     min = nodeList[left].level < nodeList[right].level ? left : right;
                 }
 
                 //如果parent节点小于它的某个子节点的话，此时筛操作
                 if (nodeList[parent].level > nodeList[min].level)
                 {
                     //子节点和父节点进行交换操作
                     var temp = nodeList[parent];
                     nodeList[parent] = nodeList[min];
                     nodeList[min] = temp;
 
                     //继续进行更下一层的过滤
                     parent = min;
                 }
                 else
                 {
                     break;
                 }
             }
         }
         #endregion
 
         #region 获取元素并下降到指定的level级别
         /// <summary>
         /// 获取元素并下降到指定的level级别
         /// </summary>
         /// <returns></returns>
         public HeapNode GetAndDownPriority(int level)
         {
             if (nodeList.Count == 0)
                 return null;
 
             //获取头元素
             var pop = nodeList[0];
 
             //设置指定优先级（如果为 MinValue 则为 -- 操作）
             nodeList[0].level = level == int.MinValue ? --nodeList[0].level : level;
 
             //下滤堆
             DownHeapAdjust(nodeList, 0);
 
             return nodeList[0];
         }
         #endregion
 
         #region 获取元素并下降优先级
         /// <summary>
         /// 获取元素并下降优先级
         /// </summary>
         /// <returns></returns>
         public HeapNode GetAndDownPriority()
         {
             //下降一个优先级
             return GetAndDownPriority(int.MinValue);
         }
         #endregion
 
         #region 返回当前优先队列中的元素个数
         /// <summary>
         /// 返回当前优先队列中的元素个数
         /// </summary>
         /// <returns></returns>
         public int Count()
         {
             return nodeList.Count;
         }
         #endregion
     }
 }

代码007普通

打赏 收藏 海报 链接