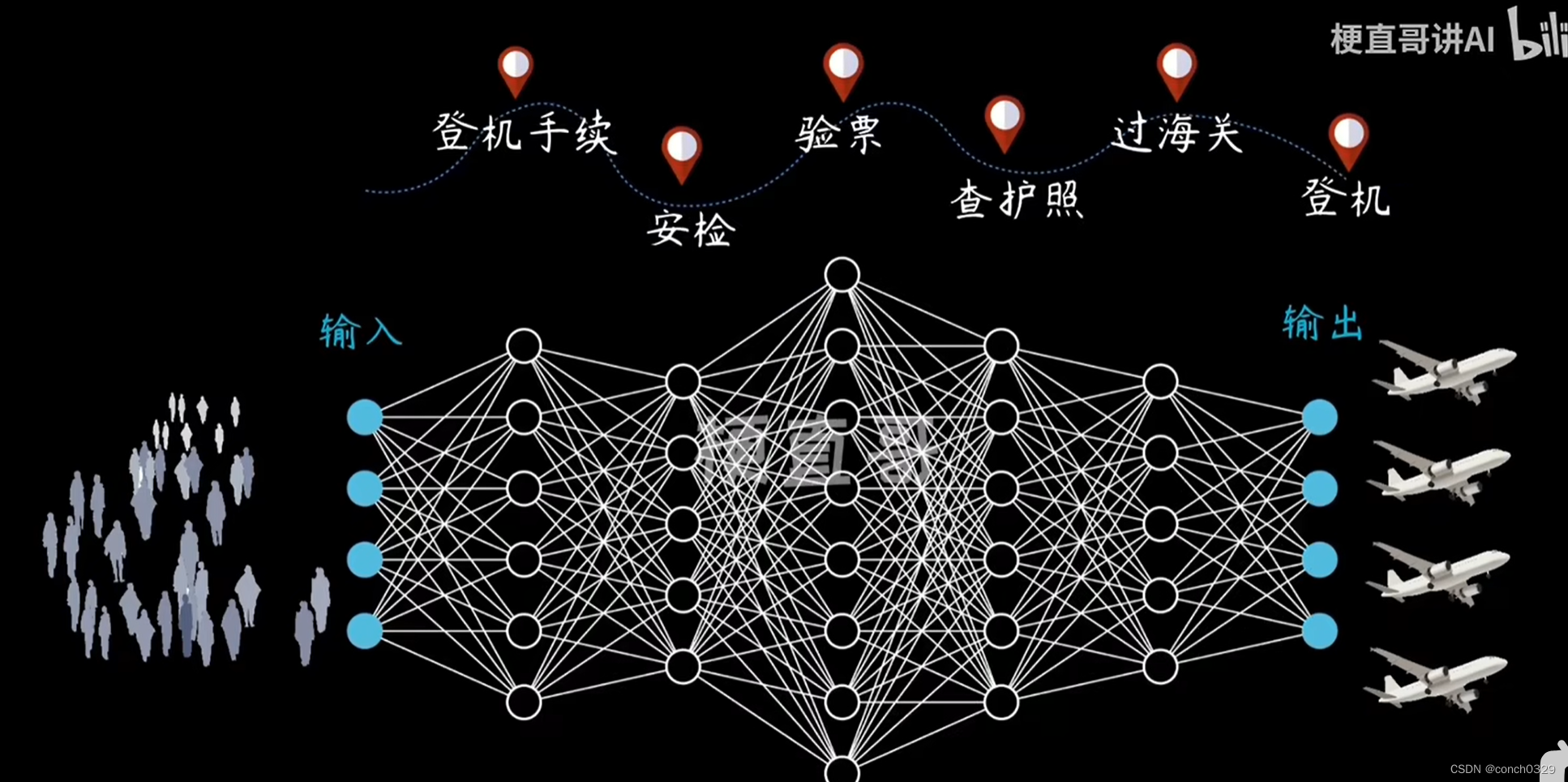
本文介绍: 语言环境:Python3.6.5编译器:jupyter notebook深度学习环境:TensorFlow2.4.1**卷积神经网络(CNN)实现mnist手写数字识别 **卷积神经网络(CNN)多种图片分类的实现卷积神经网络(CNN)衣服图像分类的实现卷积神经网络(CNN)鲜花识别**卷积神经网络(CNN)天气识别 **卷积神经网络(VGG-16)识别海贼王草帽一伙**卷积神经网络(ResNet-50)鸟类识别 **来自专栏:机器学习与深度学习算法推荐。
一、前言
我的环境:
往期精彩内容:
- 卷积神经网络(CNN)实现mnist手写数字识别
- 卷积神经网络(CNN)多种图片分类的实现
- 卷积神经网络(CNN)衣服图像分类的实现
- 卷积神经网络(CNN)鲜花识别
- 卷积神经网络(CNN)天气识别
- 卷积神经网络(VGG-16)识别海贼王草帽一伙
- 卷积神经网络(ResNet-50)鸟类识别
二、前期工作
1. 设置GPU(如果使用的是CPU可以忽略这步)
import tensorflow as tf
gpus = tf.config.list_physical_devices("GPU")
if gpus:
tf.config.experimental.set_memory_growth(gpus[0], True) #设置GPU显存用量按需使用
tf.config.set_visible_devices([gpus[0]],"GPU")
2. 导入数据
import os,math
from tensorflow.keras.layers import Dropout, Dense, SimpleRNN
from sklearn.preprocessing import MinMaxScaler
from sklearn import metrics
import numpy as np
import pandas as pd
import tensorflow as tf
import matplotlib.pyplot as plt
# 支持中文
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
data = pd.read_csv('./datasets/SH600519.csv') # 读取股票文件
data
| Unnamed: 0 | date | open | close | high | low | volume | code | |
|---|---|---|---|---|---|---|---|---|
| 0 | 74 | 2010-04-26 | 88.702 | 87.381 | 89.072 | 87.362 | 107036.13 | 600519 |
| 1 | 75 | 2010-04-27 | 87.355 | 84.841 | 87.355 | 84.681 | 58234.48 | 600519 |
| 2 | 76 | 2010-04-28 | 84.235 | 84.318 | 85.128 | 83.597 | 26287.43 | 600519 |
| 3 | 77 | 2010-04-29 | 84.592 | 85.671 | 86.315 | 84.592 | 34501.20 | 600519 |
| 4 | 78 | 2010-04-30 | 83.871 | 82.340 | 83.871 | 81.523 | 85566.70 | 600519 |
| … | … | … | … | … | … | … | … | … |
| 2421 | 2495 | 2020-04-20 | 1221.000 | 1227.300 | 1231.500 | 1216.800 | 24239.00 | 600519 |
| 2422 | 2496 | 2020-04-21 | 1221.020 | 1200.000 | 1223.990 | 1193.000 | 29224.00 | 600519 |
| 2423 | 2497 | 2020-04-22 | 1206.000 | 1244.500 | 1249.500 | 1202.220 | 44035.00 | 600519 |
| 2424 | 2498 | 2020-04-23 | 1250.000 | 1252.260 | 1265.680 | 1247.770 | 26899.00 | 600519 |
| 2425 | 2499 | 2020-04-24 | 1248.000 | 1250.560 | 1259.890 | 1235.180 | 19122.00 | 600519 |
training_set = data.iloc[0:2426 - 300, 2:3].values
test_set = data.iloc[2426 - 300:, 2:3].values
四、数据预处理
1.归一化
sc = MinMaxScaler(feature_range=(0, 1))
training_set = sc.fit_transform(training_set)
test_set = sc.transform(test_set)
2.设置测试集训练集
x_train = []
y_train = []
x_test = []
y_test = []
"""
使用前60天的开盘价作为输入特征x_train
第61天的开盘价作为输入标签y_train
for循环共构建2426-300-60=2066组训练数据。
共构建300-60=260组测试数据
"""
for i in range(60, len(training_set)):
x_train.append(training_set[i - 60:i, 0])
y_train.append(training_set[i, 0])
for i in range(60, len(test_set)):
x_test.append(test_set[i - 60:i, 0])
y_test.append(test_set[i, 0])
# 对训练集进行打乱
np.random.seed(7)
np.random.shuffle(x_train)
np.random.seed(7)
np.random.shuffle(y_train)
tf.random.set_seed(7)
"""
将训练数据调整为数组(array)
调整后的形状:
x_train:(2066, 60, 1)
y_train:(2066,)
x_test :(240, 60, 1)
y_test :(240,)
"""
x_train, y_train = np.array(x_train), np.array(y_train) # x_train形状为:(2066, 60, 1)
x_test, y_test = np.array(x_test), np.array(y_test)
"""
输入要求:[送入样本数, 循环核时间展开步数, 每个时间步输入特征个数]
"""
x_train = np.reshape(x_train, (x_train.shape[0], 60, 1))
x_test = np.reshape(x_test, (x_test.shape[0], 60, 1))
五、构建模型
model = tf.keras.Sequential([
SimpleRNN(80, return_sequences=True), #布尔值。是返回输出序列中的最后一个输出,还是全部序列。
Dropout(0.2), #防止过拟合
SimpleRNN(80),
Dropout(0.2),
Dense(1)
])
六、激活模型
# 该应用只观测loss数值,不观测准确率,所以删去metrics选项,一会在每个epoch迭代显示时只显示loss值
model.compile(optimizer=tf.keras.optimizers.Adam(0.001),
loss='mean_squared_error') # 损失函数用均方误差
七、训练模型
history = model.fit(x_train, y_train,
batch_size=64,
epochs=20,
validation_data=(x_test, y_test),
validation_freq=1) #测试的epoch间隔数
model.summary()
Epoch 1/20
33/33 [==============================] - 6s 123ms/step - loss: 0.1809 - val_loss: 0.0310
Epoch 2/20
33/33 [==============================] - 3s 105ms/step - loss: 0.0257 - val_loss: 0.0721
Epoch 3/20
33/33 [==============================] - 3s 85ms/step - loss: 0.0165 - val_loss: 0.0059
Epoch 4/20
33/33 [==============================] - 3s 85ms/step - loss: 0.0097 - val_loss: 0.0111
Epoch 5/20
33/33 [==============================] - 3s 90ms/step - loss: 0.0099 - val_loss: 0.0139
Epoch 6/20
33/33 [==============================] - 3s 105ms/step - loss: 0.0067 - val_loss: 0.0167
Epoch 7/20
33/33 [==============================] - 3s 86ms/step - loss: 0.0067 - val_loss: 0.0095
Epoch 8/20
33/33 [==============================] - 3s 91ms/step - loss: 0.0063 - val_loss: 0.0218
Epoch 9/20
33/33 [==============================] - 3s 99ms/step - loss: 0.0052 - val_loss: 0.0109
Epoch 10/20
33/33 [==============================] - 3s 99ms/step - loss: 0.0043 - val_loss: 0.0120
Epoch 11/20
33/33 [==============================] - 3s 92ms/step - loss: 0.0044 - val_loss: 0.0167
Epoch 12/20
33/33 [==============================] - 3s 89ms/step - loss: 0.0039 - val_loss: 0.0032
Epoch 13/20
33/33 [==============================] - 3s 88ms/step - loss: 0.0041 - val_loss: 0.0052
Epoch 14/20
33/33 [==============================] - 3s 93ms/step - loss: 0.0035 - val_loss: 0.0179
Epoch 15/20
33/33 [==============================] - 4s 110ms/step - loss: 0.0033 - val_loss: 0.0124
Epoch 16/20
33/33 [==============================] - 3s 95ms/step - loss: 0.0035 - val_loss: 0.0149
Epoch 17/20
33/33 [==============================] - 4s 111ms/step - loss: 0.0028 - val_loss: 0.0111
Epoch 18/20
33/33 [==============================] - 4s 110ms/step - loss: 0.0029 - val_loss: 0.0061
Epoch 19/20
33/33 [==============================] - 3s 104ms/step - loss: 0.0027 - val_loss: 0.0110
Epoch 20/20
33/33 [==============================] - 3s 90ms/step - loss: 0.0028 - val_loss: 0.0037
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
simple_rnn (SimpleRNN) (None, 60, 80) 6560
_________________________________________________________________
dropout (Dropout) (None, 60, 80) 0
_________________________________________________________________
simple_rnn_1 (SimpleRNN) (None, 80) 12880
_________________________________________________________________
dropout_1 (Dropout) (None, 80) 0
_________________________________________________________________
dense (Dense) (None, 1) 81
=================================================================
Total params: 19,521
Trainable params: 19,521
Non-trainable params: 0
_________________________________________________________________
八、结果可视化
1.绘制loss图
plt.plot(history.history['loss'] , label='Training Loss')
plt.plot(history.history['val_loss'], label='Validation Loss')
plt.legend()
plt.show()
2.预测
predicted_stock_price = model.predict(x_test) # 测试集输入模型进行预测
predicted_stock_price = sc.inverse_transform(predicted_stock_price) # 对预测数据还原---从(0,1)反归一化到原始范围
real_stock_price = sc.inverse_transform(test_set[60:]) # 对真实数据还原---从(0,1)反归一化到原始范围
# 画出真实数据和预测数据的对比曲线
plt.plot(real_stock_price, color='red', label='Stock Price')
plt.plot(predicted_stock_price, color='blue', label='Predicted Stock Price')
plt.title('Stock Price Prediction by K同学啊')
plt.xlabel('Time')
plt.ylabel('Stock Price')
plt.legend()
plt.show()
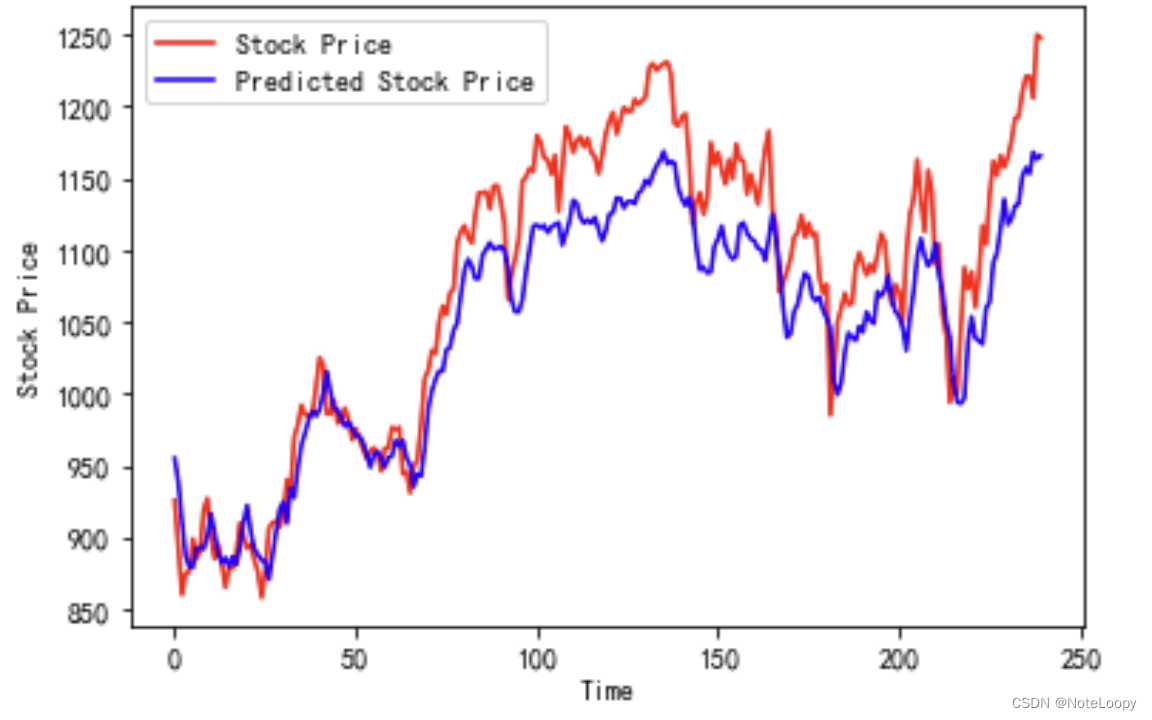
3.评估
MSE = metrics.mean_squared_error(predicted_stock_price, real_stock_price)
RMSE = metrics.mean_squared_error(predicted_stock_price, real_stock_price)**0.5
MAE = metrics.mean_absolute_error(predicted_stock_price, real_stock_price)
R2 = metrics.r2_score(predicted_stock_price, real_stock_price)
print('均方误差: %.5f' % MSE)
print('均方根误差: %.5f' % RMSE)
print('平均绝对误差: %.5f' % MAE)
print('R2: %.5f' % R2)
均方误差: 1833.92534
均方根误差: 42.82435
平均绝对误差: 36.23424
R2: 0.72347
原文地址:https://blog.csdn.net/weixin_45822638/article/details/134545938
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_8339.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!
主题授权提示:请在后台主题设置-主题授权-激活主题的正版授权,授权购买:RiTheme官网
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。