数据结构 — 图论之最小生成树

1.最小生成树算法

定义:最小生成树算法:连通图有n个顶点组成,那么此时的图的每一个点都能相互连接并且边的个数为n-1条,那么此时该图就是最小生成树.

下面量算法有几个共同的特点:

1.只能使用图中权值最小的边来构造生成树

2.只能使用恰好n-1条边构造生成树

3.n-1条边的图不能存在回路

4.Krusk al和Prim 两个算法都采用了逐步求解的贪心策略

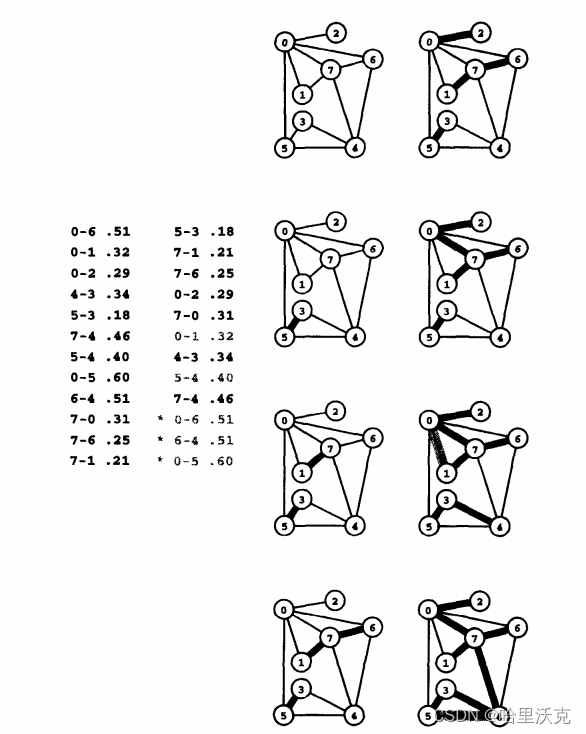
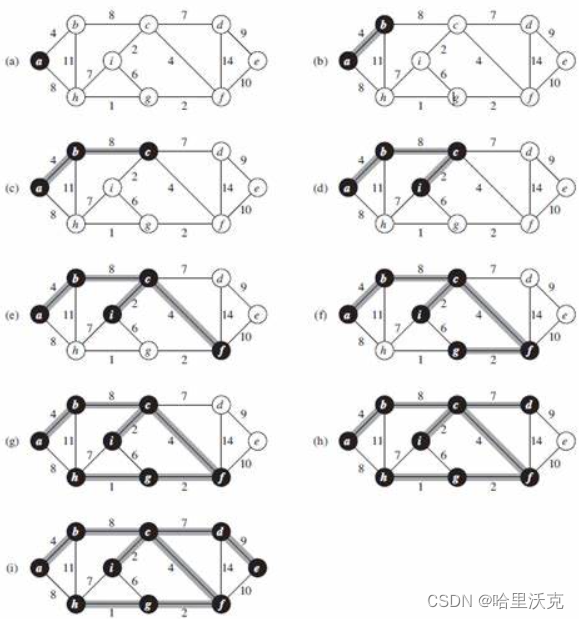
1.Krusk al算法

任给一个有n个顶点的连通网络N={V,E}，首先构造一个由这n个顶点组成、不含任何边的图G={V,NULL}，其中每个顶点自成一个连通分量，其次不断从E中取出权值最小的一条边(若有多条任取其一)，若该边的两个顶点来自不同的连通分量，则将此边加入到G中。如此重复，直到所有顶点在同一个连通分量上为止。核心：每次迭代时，选出一条具有最小权值，且两端点不在同一连通分量上的边，加入生成树。
		//数组的下标添加边
		void _AddEdge(size_t srci, size_t dsti, const W&amp; w)
		{
			_matrix[srci][dsti] = w;
			// 无向图
			if (Direction == false)
			{
				_matrix[dsti][srci] = w;
			}
		}

		struct Edge
		{
			size_t _srci;
			size_t _dsti;
			W _w;

			Edge(size_t srci, size_t dsti, const W&amp; w)
				:_srci(srci)
				, _dsti(dsti)
				, _w(w)
			{}

			bool operator&gt;(const Edge _edge)const
			{
				return _w > e._w;
			}
		};

		W Kruskal(Self&amp; minTree)
		{
			size_t n = _vertexs.size();
			
			minTree._vertexs = _vertexs;
			minTree._indexMap = _indexMap;
			minTree._matrix.resize(n);
			for (size_t i = 0; i < n; ++i)
			{
				minTree._matrix[i].resize(n, MAX_W);
			}

			priority_queue<Edge, vector<Edge>, greater<Edge>> minque;
			for (size_t i = 0; i < n; ++i)
			{
				for (size_t j = 0; j < n; ++j)
				{
					if (i < j &amp;&amp; _matrix[i][j] != MAX_W)
					{
						minque.push(Edge(i, j, _matrix[i][j]));
					}
				}
			}

			int size = 0;
			W totalW = W();
			UnionFindSet ufs(n);
			while (!minque.empty())
			{
				Edge min = minque.top();
				minque.pop();

				if (!ufs.InSet(min._srci, min._dsti))
				{
					minTree._AddEdge(min._srci, min._dsti, min._w);
					ufs.Union(min._srci, min._dsti);
					++size;
					totalW += min._w;
				}
			}
			if (size == n - 1)
				return totalW;
			else
				return W();
		}
2.Prim算法

1.从源点出发，将所有与源点连接的点加入一个待处理的集合中

2.从集合中找出与源点的边中权重最小的点，从待处理的集合中移除标记为确定的点

3.将找到的点按照步骤1的方式处理

4.重复2，3步直到所有的点都被标记

(重点是不需要并查集来判断是否成环,因为两个集合就天然区分是否成环的因素)
		W Prim(Self&amp; minTree,const V& src)
		{
			size_t srci = GetVertexIndex(src);
			size_t n = _vertexs.size();

			minTree._vertexs = _vertexs;
			minTree._indexMap = _indexMap;
			minTree._matrix.resize(n);
			for (size_t i = 0; i < n; ++i)
			{
				minTree._matrix[i].resize(n, MAX_W);
			}

			vector<bool> X(n, false);
			vector<bool> Y(n, true);
			X[srci] = true;
			Y[srci] = false;

			priority_queue<Edge, vector<Edge>, greater<Edge>> minq;
			for (int i = 0; i < n; ++i)
			{
				if (_matrix[srci][i] != MAX_W)
				{
					minq.push(Edge(srci, i, _matrix[srci][i]);
				}
			}

			size_t num = 0;
			W sum = W();
			while (!minq.empty())
			{
				Edge min = minq.top();
				minq.pop();
				if (!X[min._dsti])
				{
					minTree.AddEdge(min._srci, min._dsti, min._w);
					X.insert(min._dsti);
					Y.erase(min._dsti);
					++num;
					sum += min._w;
					if (num == n - 1) break;

					for (int i = 0; i < n; ++i)
					{
						if (_matrix[min._dsti][i] != MAX_W && Y[i])
						{
							minq.push(Edge(min._dsti, i, _matrix[min._dsti][i]);
						}
					}
				}
			}
			if (num == n - 1)
				return sum;
			else
				return W();
		}