LeetCode63. Unique Paths II

本文介绍: 【代码】LeetCode63. Unique Pa t h s II。

文章 目录

- 一、题目
- 二、题解

一、题目

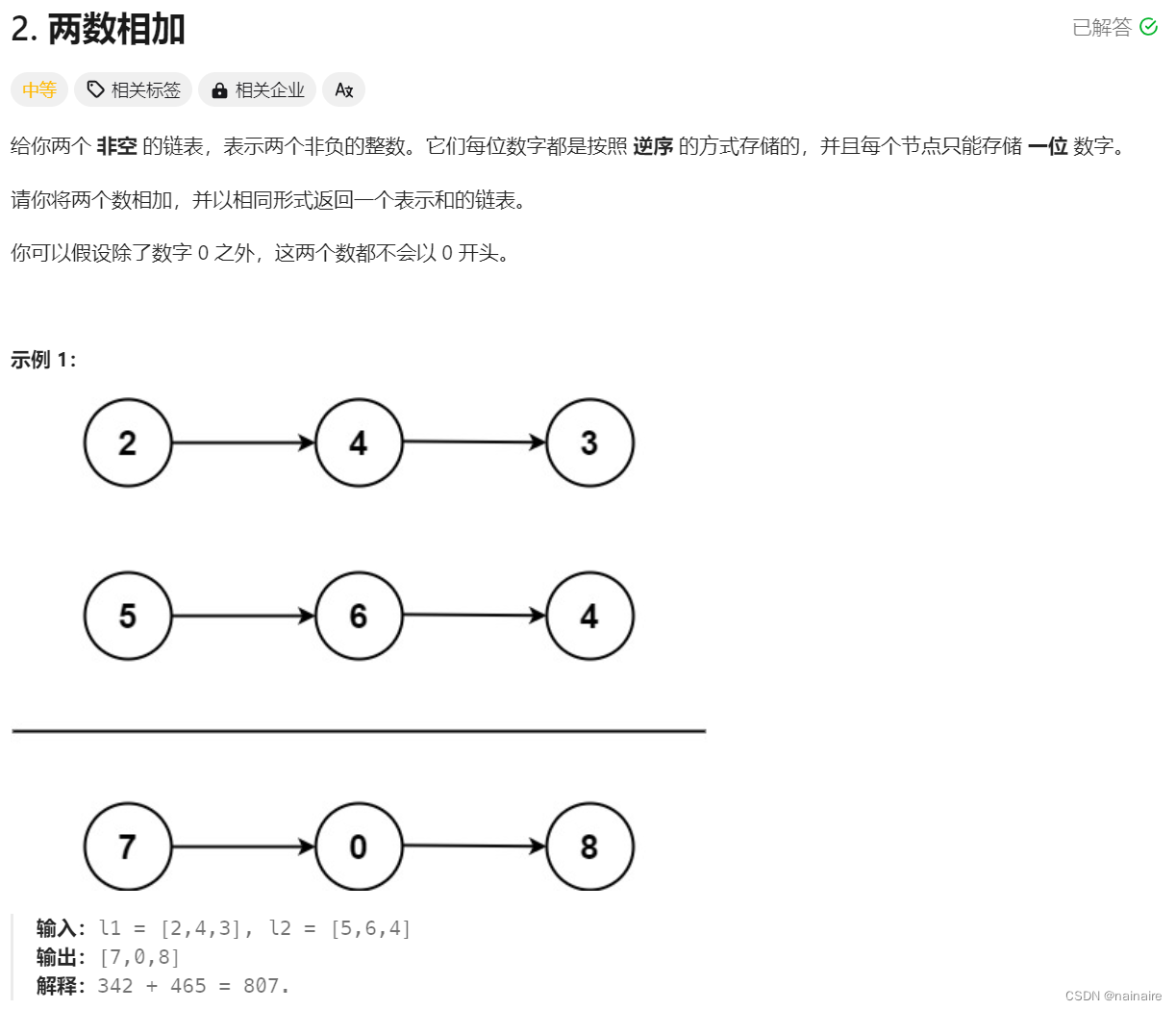
You are given an m x n integer array grid. There is a robot initially located a t t he top–left corner (i.e., grid[0][0]). The robot tries to move to t he bottom-right corner (i.e., grid[m – 1][n – 1]). The robot can only move either down or right at any point in time.

An ob stacle and s p a ce are mar ked as 1 or 0 respectiv ely in grid. A path that the robot takes ca nnot include any square that is an obstacle.

Return the number of p ossible unique paths that the robot can take to reach the bottom-right corner.

The test cases are generated so that the answer will be less than or equal to 2 * 109.

Ex ample 1:

Input: obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
Output: 2
Ex p lanation: There is one obstacle in the mid dle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:

Right -> Right -> Down -> Down
Down -> Down -> Right -> Right
Ex ample 2:

Input: obstacleGrid = [[0,1],[0,0]]
Output: 1

Constrain ts:

m == obstacleGrid.length
n == obstacleGrid[i].length
1 <= m, n <= 100
obstacleGrid[i][j] is 0 or 1.

二、题解

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>&amp; obstacleGrid) {
        int m = obstacleGrid.size();
        int n = obstacleGrid[0].size();
        vector<vector<int>> dp(m,vector<int>(n,0));
        //初始化dp数组
        for(int i = 0;i < m;i++){
            if(obstacleGrid[i][0] == 0) dp[i][0] = 1;
            else break;
        }
        for(int j = 0;j < n;j++){
            if(obstacleGrid[0][j] == 0) dp[0][j] = 1;
            else break;
        }
        for(int i = 1;i < m;i++){
            for(int j = 1;j < n;j++){
                if(obstacleGrid[i][j] == 1) dp[i][j] = 0;
                else dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
};